| title | date | tags | ||
|---|---|---|---|---|
统计可能的树根数目---LeetCode2581(换根dp) |
2023-03-07 06:30:04 -0800 |
|
日期: 2023-03-07
Alice 有一棵 n 个节点的树,节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示,其中 edges[i] = [ai, bi] ,表示树中节点 ai 和 bi 之间有一条边。
Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测,Bob 做如下事情:
选择两个 不相等 的整数 u 和 v ,且树中必须存在边 [u, v] 。 Bob 猜测树中 u 是 v 的 父节点 。 Bob 的猜测用二维整数数组 guesses 表示,其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。
Alice 非常懒,她不想逐个回答 Bob 的猜测,只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。
给你二维整数数组 edges ,Bob 的所有猜测和整数 k ,请你返回可能成为树根的 节点数目 。如果没有这样的树,则返回 0。
输入:edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出:3
解释:
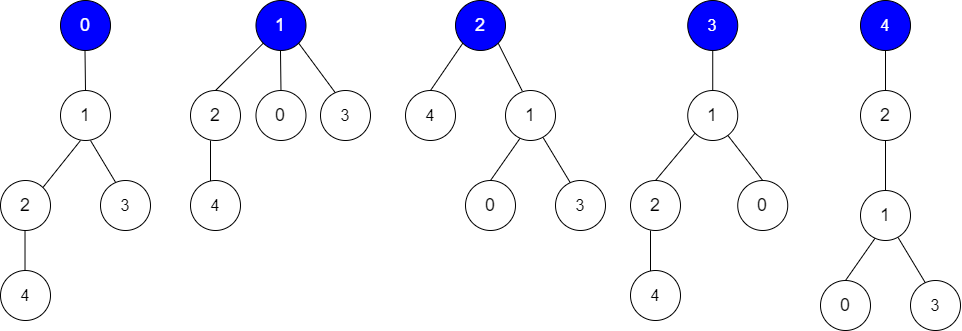
根为节点 0 ,正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ,正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ,正确的猜测为 [1,0], [2,4]
根为节点 4 ,正确的猜测为 [1,3], [1,0]
节点 0 ,1 或 2 为根时,可以得到 3 个正确的猜测。
换根dp就是先算出来一个答案。
然后再根据根之间的递推关系来算出其他的答案,其实也不能说是dp,感觉其实就是两个dfs。
这里就是先算出一个答案,那么另外一个的答案就是 cnt - m[node][to] + m[to][node],因为之前的就是猜错了,现在的就是猜对了。
class Solution {
public:
int cnt0 = 0;
int ans = 0;
int K;
void dfs(int node, int far, vector<vector<int>>& g, map<pair<int,int>,int>& m){
if(m.count(make_pair(far,node)) > 0){
cnt0 += m[make_pair(far,node)];
}
for(int to:g[node]){
if(to != far){
dfs(to,node,g,m);
}
}
}
void reroot(int node, int far, int cnt, vector<vector<int>>& g, map<pair<int,int>,int>& m){
if(cnt >= K) ans += 1;
for(int to:g[node]){
if(to != far){
reroot(to,node, cnt - m[make_pair(node,to)] + m[make_pair(to,node)],g,m);
}
}
}
int rootCount(vector<vector<int>>& edges, vector<vector<int>>& guesses, int k) {
// edges转邻接表
int len = edges.size();
vector<vector<int>> g(len+1);
for(auto& x:edges){
g[x[0]].push_back(x[1]);
g[x[1]].push_back(x[0]);
}
//guesses转哈希
map<pair<int,int>,int> m;
for(auto& x:guesses){
m[make_pair(x[0],x[1])] = 1;
}
dfs(0,-1,g,m);
K = k;
reroot(0,-1,cnt0,g,m);
return ans;
}
};