diff --git a/SUMMARY.md b/SUMMARY.md
deleted file mode 100644
index 66254d8..0000000
--- a/SUMMARY.md
+++ /dev/null
@@ -1,172 +0,0 @@
-# Summary
-
-* [Introduction](README.md)
-* [About me](aboutme.md)
-* [归档](archive.md)
-* [计算机图形学](CG/README.md)
- * [MicroRenderer](CG/SoftRasterizer/README.md)
- * [(一) 渲染管线](CG/SoftRasterizer/pipeline.md)
- * [(二) 进入三维](CG/SoftRasterizer/3d.md)
- * [(三) 着色模型](CG/SoftRasterizer/shading.md)
- * [GAMES101](CG/GAMES101/README.md)
- * [Assignment1](CG/GAMES101/assignment1.md)
- * [Assignment2](CG/GAMES101/assignment2.md)
- * [Assignment3](CG/GAMES101/assignment3.md)
- * [Assignment4](CG/GAMES101/assignment4.md)
- * [Assignment5](CG/GAMES101/assignment5.md)
- * [Assignment6](CG/GAMES101/assignment6.md)
- * [Assignment7](CG/GAMES101/assignment7.md)
- * [GAMES202](CG/GAMES202/README.md)
- * [Assignment1](CG/GAMES202/assignment1.md)
- * [OpenGL](CG/OpenGL/README.md)
- * [使用assimp读取没有贴图的模型](CG/OpenGL/assimp_material.md)
- * [如何将imgui跑起来](CG/imgui_run.md)
- * [我不想用imgui了](CG/imgui_giveup.md)
-
-* [ML/DL/RL](MLDLRL/README.md)
- * [机器学习](MLDLRL/ML/README.md)
- * [KNN计算的三种姿势](MLDLRL/ML/knn-distance-computing.md)
- * [用scatter函数计算onehot](MLDLRL/ML/scatter_onehot.md)
- * [深度学习](MLDLRL/DL/README.md)
- * [mac pytorch mps尝鲜](MLDLRL/DL/pytorch-mps.md)
- * [使用larq对BNN从训练到部署](MLDLRL/DL/bnndemo.md)
- * [强化学习](MLDLRL/RL/README.md)
- * [value&policy iteration](MLDLRL/RL/value&policy_iteration.md)
-* [CPP](./CPP/README.md)
- * [一些CPP简单的提速方法](./CPP/compiler_speedUp.md)
- * [手写一个vector](./CPP/handcrafted_vector.md)
-* [分布式系统](DistributedSys/README.md)
- * [MIT6.824](DistributedSys/mit6.824/readme.md)
- * [lab1-mapreduce](DistributedSys/mit6.824/lab1.md)
-
-* [Debug日常](Debug/readme.md)
- * [pybind内存泄漏](Debug/pybind内存泄漏.md)
- * [cuda和cpu的计算误差](Debug/cuda和cpu的计算误差.md)
-* [折腾](折腾/readme.md)
- * [给博客加了个归档页](折腾/blog-archive.md)
-* [算法](./algorithms/README.md)
- * [tag汇总](./algorithms/tag_table.md)
- * [LeetCode](./algorithms/LeetCode/README.md)
- * [LeetCode03](./algorithms/LeetCode/LeetCode03.md)
- * [LeetCode04](./algorithms/LeetCode/LeetCode04.md)
- * [LeetCode05](./algorithms/LeetCode/LeetCode05.md)
- * [LeetCode11](./algorithms/LeetCode/LeetCode11.md)
- * [LeetCode23](./algorithms/LeetCode/LeetCode23.md)
- * [LeetCode25](./algorithms/LeetCode/LeetCode25.md)
- * [LeetCode31](./algorithms/LeetCode/LeetCode31.md)
- * [LeetCode32](./algorithms/LeetCode/LeetCode32.md)
- * [LeetCode37](./algorithms/LeetCode/LeetCode37.md)
- * [LeetCode39](./algorithms/LeetCode/LeetCode39.md)
- * [LeetCode40](./algorithms/LeetCode/LeetCode40.md)
- * [LeetCode44](./algorithms/LeetCode/LeetCode44.md)
- * [LeetCode45](./algorithms/LeetCode/LeetCode45.md)
- * [LeetCode47](./algorithms/LeetCode/LeetCode47.md)
- * [LeetCode50](./algorithms/LeetCode/LeetCode50.md)
- * [LeetCode51](./algorithms/LeetCode/LeetCode51.md)
- * [LeetCode60](./algorithms/LeetCode/LeetCode60.md)
- * [LeetCode69](./algorithms/LeetCode/LeetCode69.md)
- * [LeetCode77](./algorithms/LeetCode/LeetCode77.md)
- * [LeetCode84](./algorithms/LeetCode/LeetCode84.md)
- * [LeetCode94](./algorithms/LeetCode/LeetCode94.md)
- * [LeetCode95](./algorithms/LeetCode/LeetCode95.md)
- * [LeetCode98](./algorithms/LeetCode/LeetCode98.md)
- * [LeetCode99](./algorithms/LeetCode/LeetCode99.md)
- * [LeetCode102](./algorithms/LeetCode/LeetCode102.md)
- * [LeetCode105](./algorithms/LeetCode/LeetCode105.md)
- * [LeetCode109](./algorithms/LeetCode/LeetCode109.md)
- * [LeetCode110](./algorithms/LeetCode/LeetCode110.md)
- * [LeetCode121](./algorithms/LeetCode/LeetCode121.md)
- * [LeetCode124](./algorithms/LeetCode/LeetCode124.md)
- * [LeetCode134](./algorithms/LeetCode/LeetCode134.md)
- * [LeetCode139](./algorithms/LeetCode/LeetCode139.md)
- * [LeetCode144](./algorithms/LeetCode/LeetCode144.md)
- * [LeetCode146](./algorithms/LeetCode/LeetCode146.md)
- * [LeetCode148](./algorithms/LeetCode/LeetCode148.md)
- * [LeetCode152](./algorithms/LeetCode/LeetCode152.md)
- * [LeetCode153](./algorithms/LeetCode/LeetCode153.md)
- * [LeetCode167](./algorithms/LeetCode/LeetCode167.md)
- * [LeetCode198](./algorithms/LeetCode/LeetCode198.md)
- * [LeetCode199](./algorithms/LeetCode/LeetCode199.md)
- * [LeetCode202](./algorithms/LeetCode/LeetCode202.md)
- * [LeetCode210](./algorithms/LeetCode/LeetCode210.md)
- * [LeetCode214](./algorithms/LeetCode/LeetCode214.md)
- * [LeetCode216](./algorithms/LeetCode/LeetCode216.md)
- * [LeetCode221](./algorithms/LeetCode/LeetCode221.md)
- * [LeetCode279](./algorithms/LeetCode/LeetCode279.md)
- * [LeetCode236](./algorithms/LeetCode/LeetCode236.md)
- * [LeetCode287](./algorithms/LeetCode/LeetCode287.md)
- * [LeetCode301](./algorithms/LeetCode/LeetCode301.md)
- * [LeetCode312](./algorithms/LeetCode/LeetCode312.md)
- * [LeetCode322](./algorithms/LeetCode/LeetCode322.md)
- * [LeetCode332](./algorithms/LeetCode/LeetCode332.md)
- * [LeetCode337](./algorithms/LeetCode/LeetCode337.md)
- * [LeetCode347](./algorithms/LeetCode/LeetCode347.md)
- * [LeetCode377](./algorithms/LeetCode/LeetCode377.md)
- * [LeetCode394](./algorithms/LeetCode/LeetCode394.md)
- * [LeetCode410](./algorithms/LeetCode/LeetCode410.md)
- * [LeetCode410](./algorithms/LeetCode/LeetCode416.md)
- * [LeetCode417](./algorithms/LeetCode/LeetCode417.md)
- * [LeetCode427](./algorithms/LeetCode/LeetCode427.md)
- * [LeetCode428](./algorithms/LeetCode/LeetCode428.md)
- * [LeetCode433](./algorithms/LeetCode/LeetCode433.md)
- * [LeetCode445](./algorithms/LeetCode/LeetCode445.md)
- * [LeetCode486](./algorithms/LeetCode/LeetCode486.md)
- * [LeetCode491](./algorithms/LeetCode/LeetCode491.md)
- * [LeetCode491](./algorithms/LeetCode/LeetCode494.md)
- * [LeetCode518](./algorithms/LeetCode/LeetCode518.md)
- * [LeetCode538](./algorithms/LeetCode/LeetCode538.md)
- * [LeetCode547](./algorithms/LeetCode/LeetCode547.md)
- * [LeetCode560](./algorithms/LeetCode/LeetCode560.md)
- * [LeetCode572](./algorithms/LeetCode/LeetCode572.md)
- * [LeetCode679](./algorithms/LeetCode/LeetCode679.md)
- * [LeetCode780](./algorithms/LeetCode/LeetCode780.md)
- * [LeetCode854](./algorithms/LeetCode/LeetCode854.md)
- * [LeetCode974](./algorithms/LeetCode/LeetCode974.md)
- * [LeetCode983](./algorithms/LeetCode/LeetCode983.md)
- * [LeetCode1025](./algorithms/LeetCode/LeetCode1025.md)
- * [LeetCode1025](./algorithms/LeetCode/LeetCode1049.md)
- * [LeetCode1095](./algorithms/LeetCode/LeetCode1095.md)
- * [LeetCode1371](./algorithms/LeetCode/LeetCode1371.md)
- * [LeetCode1458](./algorithms/LeetCode/LeetCode1458.md)
- * [LeetCode1617](./algorithms/LeetCode/LeetCode1617.md)
- * [LeetCode1823](./algorithms/LeetCode/LeetCode1823.md)
- * [LeetCode2385](./algorithms/LeetCode/LeetCode2585.md)
- * [LeetCode2395](./algorithms/LeetCode/LeetCode2395.md)
- * [LeetCode2400](./algorithms/LeetCode/LeetCode2400.md)
- * [LeetCode2528](./algorithms/LeetCode/LeetCode2528.md)
- * [LeetCode2560](./algorithms/LeetCode/LeetCode2560.md)
- * [LeetCode2581](./algorithms/LeetCode/LeetCode2581.md)
- * [LeetCode2866](./algorithms/LeetCode/LeetCode2866.md)
- * [LeetCode2867](./algorithms/LeetCode/LeetCode2867.md)
- * [LeetCode5393](./algorithms/LeetCode/LeetCode5393.md)
- * [LeetCode5394](./algorithms/LeetCode/LeetCode5394.md)
- * [LeetCode5400](./algorithms/LeetCode/LeetCode5400.md)
- * [LeetCode5402](./algorithms/LeetCode/LeetCode5402.md)
- * [LeetCode5406](./algorithms/LeetCode/LeetCode5406.md)
- * [LeetCode5413](./algorithms/LeetCode/LeetCode5413.md)
- * [LeetCode5414](./algorithms/LeetCode/LeetCode5414.md)
- * [LeetCode5474](./algorithms/LeetCode/LeetCode5474.md)
- * [LeetCode5476](./algorithms/LeetCode/LeetCode5476.md)
- * [LeetCode5477](./algorithms/LeetCode/LeetCode5477.md)
- * [LeetCode5480](./algorithms/LeetCode/LeetCode5480.md)
- * [LeetCode5500](./algorithms/LeetCode/LeetCode5500.md)
- * [LeetCode6190](./algorithms/LeetCode/LeetCode6190.md)
- * [LeetCode-jz11](./algorithms/LeetCode/LeetCode-jz11.md)
- * [LeetCode-jz51](./algorithms/LeetCode/LeetCode-jz51.md)
- * [LeetCode-m56](./algorithms/LeetCode/LeetCode-m56.md)
- * [LeetCode-LCP13](./algorithms/LeetCode/LeetCode-LCP13.md)
- * [LeetCode-LCP64](./algorithms/LeetCode/LeetCode-LCP64.md)
- * [LeetCodejz-coins](./algorithms/LeetCode/LeetCode-coins.md)
- * [LeetCode-weekly205](./algorithms/LeetCode/LeetCode-weekly205.md)
- * [LeetCode-FallContest2020](./algorithms/LeetCode/LeetCode-FallContest2020.md)
- * [LeetCode-FallContest2022](./algorithms/LeetCode/LeetCode-FallContest2022.md)
- * [CodeForces](./algorithms/CodeForces/README.md)
- * [Decreasing String](./algorithms/CodeForces/dict_order.md)
- * [AtCoder](./algorithms/Atcoder/README.md)
- * [Our clients, please wait a moment](./algorithms/AtCoder/abc325_e.md)
-
-
-
-
-
-
diff --git a/aboutme.md b/aboutme.md
deleted file mode 100644
index d98c53f..0000000
--- a/aboutme.md
+++ /dev/null
@@ -1,35 +0,0 @@
-# About me
-
-Hi, I'm Junhua Long, currently a third-year master's student in Sun Yat-sen University. I'm expected to graduate in Summer 2024.
-
-I'm broadly interested in backend/infrastructure development, computer graphics and point cloud processing.
-
-
-
-## Educations
-
-- Master of Engineering in 2024, School of Computer Science and Engineering
-
- **Sun Yat-sen University**, Guangzhou, China, 09/2021 – 06/2024 (expected)
-
-- Bachelor of Engineering, School of Computer Science
-
- **Chongqing University**, Chongqing, China, 09/2017 – 06/2021
-
-
-
-## Publications
-
-- **OctFormer: Efficient Octree-based Transformer for Point Cloud Compression with Local Enhancement**
-
- Mingyue Cui, **Junhua Long**, Mingjian Feng, Boyang Li, Kai Huang. (student first author)
-
- *Proceedings of the AAAI Conference on Artificial Intelligence. 2023 (Oral)*
-
-
-
-## Contacts
-
-Email: [a674478778@gmail.com](mailto:a674478778@gmail.com)
-
-GitHub: https://github.com/LJHG
diff --git a/algorithmArchive.json b/algorithmArchive.json
deleted file mode 100644
index 2b6901d..0000000
--- a/algorithmArchive.json
+++ /dev/null
@@ -1 +0,0 @@
-{"未归档": [{"title": "tag_table", "url": "./algorithms/tag_table.html", "date": "未指定日期"}], "2023": [{"title": " 找出强数对的最大异或值---LeetCode2395(字典树)", "url": "./algorithms/LeetCode/LeetCode2395.html", "date": "2023-11-14"}, {"title": " Dijkstra最短路,以及2N节点", "url": "./algorithms/AtCoder/abc325_e.html", "date": "2023-10-23"}, {"title": " 统计子树中城市最大距离---LeetCode1617(子集+树形dp)", "url": "./algorithms/LeetCode/LeetCode1617.html", "date": "2023-10-20"}, {"title": " 删除一个元素让字典序最小", "url": "./algorithms/CodeForces/dict_order.html", "date": "2023-10-11"}, {"title": " 找到字符串中所有字符异位词---LeetCode428(双指针哈希表)", "url": "./algorithms/LeetCode/LeetCode428.html", "date": "2023-10-04"}, {"title": " 字符串解码---LeetCode394(栈)", "url": "./algorithms/LeetCode/LeetCode394.html", "date": "2023-09-28"}, {"title": " 统计树中的合法路径数目---LeetCode2867(树形dp)", "url": "./algorithms/LeetCode/LeetCode2867.html", "date": "2023-09-27"}, {"title": " 美丽塔---LeetCode2866(单调栈)", "url": "./algorithms/LeetCode/LeetCode2866.html", "date": "2023-09-26"}, {"title": " 排序链表---LeetCode148", "url": "./algorithms/LeetCode/LeetCode148.html", "date": "2023-09-17"}, {"title": " 二叉树里的最大路径和---LeetCode124(别再错了)", "url": "./algorithms/LeetCode/LeetCode124.html", "date": "2023-08-05"}, {"title": " 二分红蓝染色法---LeetCode153等", "url": "./algorithms/LeetCode/LeetCode153.html", "date": "2023-07-22"}, {"title": " 零钱兑换---LeetCode322(完全背包)", "url": "./algorithms/LeetCode/LeetCode322.html", "date": "2023-04-01"}, {"title": " 二分枚举答案判定系列---LeetCode2528等", "url": "./algorithms/LeetCode/LeetCode2528.html", "date": "2023-03-08"}, {"title": " 二叉树灯饰---LeetCode-LCP64(树形dp 记忆化搜索)", "url": "./algorithms/LeetCode/LeetCode-LCP64.html", "date": "2023-03-07"}, {"title": " 获得分数的方法数---LeetCode2585(分组背包模板)", "url": "./algorithms/LeetCode/LeetCode2585.html", "date": "2023-03-07"}, {"title": " 统计可能的树根数目---LeetCode2581(换根dp)", "url": "./algorithms/LeetCode/LeetCode2581.html", "date": "2023-03-07"}, {"title": " 打家劫舍 IV---LeetCode2560(二分+dp)", "url": "./algorithms/LeetCode/LeetCode2560.html", "date": "2023-02-28"}, {"title": " 买卖股票的最佳时机---LeetCode121(dp)", "url": "./algorithms/LeetCode/LeetCode121.html", "date": "2023-02-26"}, {"title": " 打家劫舍III---LeetCode337(树形dp)", "url": "./algorithms/LeetCode/LeetCode337.html", "date": "2023-02-24"}, {"title": " 打家劫舍 I&II---LeetCode198&213", "url": "./algorithms/LeetCode/LeetCode198.html", "date": "2023-02-24"}, {"title": " 单词拆分---LeetCode139(背包和字符串)", "url": "./algorithms/LeetCode/LeetCode139.html", "date": "2023-02-20"}, {"title": " 组合总和 Ⅳ---LeetCode377(完全背包变体)", "url": "./algorithms/LeetCode/LeetCode377.html", "date": "2023-02-18"}, {"title": " 零钱兑换 II---LeetCode518(完全背包)", "url": "./algorithms/LeetCode/LeetCode518.html", "date": "2023-02-16"}, {"title": " 目标和---LeetCode49(不太典型的背包)", "url": "./algorithms/LeetCode/LeetCode494.html", "date": "2023-02-16"}, {"title": " 最后一块石头的重量 II---(还是背包)", "url": "./algorithms/LeetCode/LeetCode1049.html", "date": "2023-02-15"}, {"title": " 分割等和子集---LeetCode416(其实是背包问题)", "url": "./algorithms/LeetCode/LeetCode416.html", "date": "2023-02-15"}, {"title": " 重新安排行程---LeetCode332(STL)", "url": "./algorithms/LeetCode/LeetCode332.html", "date": "2023-02-10"}, {"title": " 二叉树的最近公共祖先---LeetCode236(后序遍历实现自底向上查找)", "url": "./algorithms/LeetCode/LeetCode236.html", "date": "2023-01-11"}], "2022": [{"title": " 省份数量---LeetCode547(并查集)", "url": "./algorithms/LeetCode/LeetCode547.html", "date": "2022-09-29"}, {"title": " 盛最多水的容器---LeetCode11(贪心双指针)", "url": "./algorithms/LeetCode/LeetCode11.html", "date": "2022-09-28"}, {"title": " 通配符匹配---LeetCode44(dp)", "url": "./algorithms/LeetCode/LeetCode44.html", "date": "2022-09-27"}, {"title": " 最长有效括号---LeetCode32(dp)", "url": "./algorithms/LeetCode/LeetCode32.html", "date": "2022-09-26"}, {"title": " 找到所有好下标---LeetCode6190(递推)", "url": "./algorithms/LeetCode/LeetCode6190.html", "date": "2022-09-25"}, {"title": " 2022秋季编程大赛记录", "url": "./algorithms/LeetCode/LeetCode-FallContest2022.html", "date": "2022-09-24"}, {"title": " 删除无效的括号---LeetCode301(BFS)", "url": "./algorithms/LeetCode/LeetCode301.html", "date": "2022-09-23"}, {"title": " 完全平方数---LeetCode279(DP/BFS)", "url": "./algorithms/LeetCode/LeetCode279.html", "date": "2022-09-23"}, {"title": " 恢复二叉搜索树---LeetCode99(DFS+中序遍历)", "url": "./algorithms/LeetCode/LeetCode99.html", "date": "2022-09-22"}, {"title": " 用BFS解决交换问题---LeetCode854(BFS)", "url": "./algorithms/LeetCode/LeetCode854.html", "date": "2022-09-21"}, {"title": " 恰好移动 k 步到达某一位置的方法数目---LeetCode2400(dp与预处理)", "url": "./algorithms/LeetCode/LeetCode2400.html", "date": "2022-09-06"}, {"title": " 最小基因变化---LeetCode433(bfs)", "url": "./algorithms/LeetCode/LeetCode433.html", "date": "2022-05-07"}, {"title": " 找出游戏的获胜者---LeetCode1823(队列模拟链表,数学)", "url": "./algorithms/LeetCode/LeetCode1823.html", "date": "2022-05-04"}, {"title": " 建立四叉树---LeetCode427(dfs)", "url": "./algorithms/LeetCode/LeetCode427.html", "date": "2022-04-29"}, {"title": " 太平洋大西洋水流问题---LeetCode417(dfs)", "url": "./algorithms/LeetCode/LeetCode417.html", "date": "2022-04-27"}, {"title": " 到达终点---LeetCode780", "url": "./algorithms/LeetCode/LeetCode780.html", "date": "2022-04-09"}], "2020": [{"title": " 加油站---LeetCode134(more than 模拟)", "url": "./algorithms/LeetCode/LeetCode134.html", "date": "2020-11-18"}, {"title": " 下一个排列---LeetCode31(新的思路)", "url": "./algorithms/LeetCode/LeetCode31.html", "date": "2020-11-10"}, {"title": " 二叉树的前序遍历---LeetCode144", "url": "./algorithms/LeetCode/LeetCode144.html", "date": "2020-10-27"}, {"title": " 把二叉搜索树转换为累加树---LeetCode538", "url": "./algorithms/LeetCode/LeetCode538.html", "date": "2020-09-21"}, {"title": " 全排列Ⅱ---LeetCode47(去重)", "url": "./algorithms/LeetCode/LeetCode47.html", "date": "2020-09-18"}, {"title": " 解数独---LeetCode37(优化的力量)", "url": "./algorithms/LeetCode/LeetCode37.html", "date": "2020-09-15"}, {"title": " 二叉树中序遍历---LeetCode94(递归和栈)", "url": "./algorithms/LeetCode/LeetCode94.html", "date": "2020-09-14"}, {"title": " 秋季编程大赛记录", "url": "./algorithms/LeetCode/LeetCode-FallContest2020.html", "date": "2020-09-12"}, {"title": " 组合总和3---LeetCode216", "url": "./algorithms/LeetCode/LeetCode216.html", "date": "2020-09-11"}, {"title": " 组合总和2---LeetCode40(答案去重)", "url": "./algorithms/LeetCode/LeetCode40.html", "date": "2020-09-10"}, {"title": " 组合总和---LeetCode39(wsl)", "url": "./algorithms/LeetCode/LeetCode39.html", "date": "2020-09-09"}, {"title": " 组合---LeetCode77(不小心把组合做成排列了)", "url": "./algorithms/LeetCode/LeetCode77.html", "date": "2020-09-08"}, {"title": " 前K个高频元素---LeetCode347(优先队列)", "url": "./algorithms/LeetCode/LeetCode347.html", "date": "2020-09-07"}, {"title": " 205周赛记录---(学会用map + 并查集太强了)", "url": "./algorithms/LeetCode/LeetCode-weekly205.html", "date": "2020-09-06"}, {"title": " 第k个排列---LeetCode60(优化的力量)", "url": "./algorithms/LeetCode/LeetCode60.html", "date": "2020-09-05"}, {"title": " N皇后---LeetCode51(递归和回溯还是有区别的)", "url": "./algorithms/LeetCode/LeetCode51.html", "date": "2020-09-03"}, {"title": " 预测赢家---LeetCode486(博弈)", "url": "./algorithms/LeetCode/LeetCode486.html", "date": "2020-09-01"}, {"title": " 乘积为正数的最长子数组长度---LeetCode5500", "url": "./algorithms/LeetCode/LeetCode5500.html", "date": "2020-08-30"}, {"title": " 往字符串前面添字符形成的最短回文串---LeetCode214", "url": "./algorithms/LeetCode/LeetCode214.html", "date": "2020-08-29"}, {"title": " 递增子序列---LeetCode491(dp失败QAQ)", "url": "./algorithms/LeetCode/LeetCode491.html", "date": "2020-08-25"}, {"title": " 可以到达所有点的最少点数目---LeetCode5480", "url": "./algorithms/LeetCode/LeetCode5480.html", "date": "2020-08-23"}, {"title": " 24点---LeetCode679", "url": "./algorithms/LeetCode/LeetCode679.html", "date": "2020-08-22"}, {"title": " 有序链表转换二叉搜索树---LeetCode109", "url": "./algorithms/LeetCode/LeetCode109.html", "date": "2020-08-18"}, {"title": " 平衡二叉树---LeetCode110", "url": "./algorithms/LeetCode/LeetCode110.html", "date": "2020-08-17"}, {"title": " 找出数组游戏的赢家---LeetCode5476", "url": "./algorithms/LeetCode/LeetCode5476.html", "date": "2020-08-02"}, {"title": " 排布二进制网格的最少交换次数---LeetCode5477", "url": "./algorithms/LeetCode/LeetCode5477.html", "date": "2020-08-02"}, {"title": " 寻宝---LCP13(bfs+状压dp)", "url": "./algorithms/LeetCode/LeetCode-LCP13.html", "date": "2020-07-29"}, {"title": " 好叶子节点对的数量---LeetCode5474(记录路径)", "url": "./algorithms/LeetCode/LeetCode5474.html", "date": "2020-07-26"}, {"title": " 分割数组的最大值---LeetCode410(dp)", "url": "./algorithms/LeetCode/LeetCode410.html", "date": "2020-07-25"}, {"title": " 除数博弈---LeetCode1025(智力题)", "url": "./algorithms/LeetCode/LeetCode1025.html", "date": "2020-07-24"}, {"title": " 剑指 Offer 11. 旋转数组的最小数字---(二分)", "url": "./algorithms/LeetCode/LeetCode-jz11.html", "date": "2020-07-22"}, {"title": " 不同的二叉搜索树 II---LeetCode95", "url": "./algorithms/LeetCode/LeetCode95.html", "date": "2020-07-21"}, {"title": " 两数之和 II - 输入有序数组---LeetCode167(二分或双指针)", "url": "./algorithms/LeetCode/LeetCode167.html", "date": "2020-07-20"}, {"title": " 戳气球---LeetCode312(dp)", "url": "./algorithms/LeetCode/LeetCode312.html", "date": "2020-07-19"}, {"title": " 柱状图中最大的矩形---LeetCode84(单调栈)", "url": "./algorithms/LeetCode/LeetCode84.html", "date": "2020-05-30"}, {"title": " 和可被 K 整除的子数组---LeetCode974(我数学不太好)", "url": "./algorithms/LeetCode/LeetCode974.html", "date": "2020-05-27"}, {"title": " 寻找重复数---LeetCode287(快慢指针)", "url": "./algorithms/LeetCode/LeetCode287.html", "date": "2020-05-26"}, {"title": " 两个子序列的最大点积---LeetCode1458(双序列dp)", "url": "./algorithms/LeetCode/LeetCode1458.html", "date": "2020-05-26"}, {"title": " LRU缓存机制---LeetCode146(链表好像变香了)", "url": "./algorithms/LeetCode/LeetCode146.html", "date": "2020-05-25"}, {"title": " 寻找两个正序数组的中位数---LeetCode04(噩梦级边界判断)", "url": "./algorithms/LeetCode/LeetCode04.html", "date": "2020-05-24"}, {"title": " 从前序与中序遍历序列构造二叉树---LeetCode105", "url": "./algorithms/LeetCode/LeetCode105.html", "date": "2020-05-22"}, {"title": " 每个元音包含偶数次的最长子字符串---LeetCode1371(前缀和+哈希优化+状态压缩)", "url": "./algorithms/LeetCode/LeetCode1371.html", "date": "2020-05-20"}, {"title": " 乘积最大子数组---LeetCode152(不会真的有人以为是前缀和吧)", "url": "./algorithms/LeetCode/LeetCode152.html", "date": "2020-05-18"}, {"title": " 课程表---LeetCode210(拓扑排序)", "url": "./algorithms/LeetCode/LeetCode210.html", "date": "2020-05-17"}, {"title": " 收藏清单---LeetCode5414(能线性扫就别搞两重循环了)", "url": "./algorithms/LeetCode/LeetCode5414.html", "date": "2020-05-17"}, {"title": " 重新排列句子中的单词---LeetCode5413(在排序时长度相同的保持相对位置不变)", "url": "./algorithms/LeetCode/LeetCode5413.html", "date": "2020-05-17"}, {"title": " K个一组翻转链表---LeetCode25(指针地狱)", "url": "./algorithms/LeetCode/LeetCode25.html", "date": "2020-05-16"}, {"title": " 找和为k连续子数组---LeetCode560(前缀和+哈希优化)", "url": "./algorithms/LeetCode/LeetCode560.html", "date": "2020-05-15"}, {"title": " 二叉树层序遍历----LeetCode102", "url": "./algorithms/LeetCode/LeetCode102.html", "date": "2020-05-13"}, {"title": " Pow(x,n)---LeetCode50(快速幂)", "url": "./algorithms/LeetCode/LeetCode50.html", "date": "2020-05-11"}, {"title": " 收集树上所有苹果---LeetCode5406(碰见树就GG)", "url": "./algorithms/LeetCode/LeetCode5406.html", "date": "2020-05-10"}, {"title": " LeetCode69", "url": "./algorithms/LeetCode/LeetCode69.html", "date": "2020-05-09"}, {"title": " 最大正方形---LeetCode221(能想到怎么dp就很简单的dp)", "url": "./algorithms/LeetCode/LeetCode221.html", "date": "2020-05-08"}, {"title": " 另一个树的子树---LeetCode572", "url": "./algorithms/LeetCode/LeetCode572.html", "date": "2020-05-07"}, {"title": " 最低票价---LeetCode983(简单dp)", "url": "./algorithms/LeetCode/LeetCode983.html", "date": "2020-05-06"}, {"title": " 验证二叉搜索树---LeetCode98", "url": "./algorithms/LeetCode/LeetCode98.html", "date": "2020-05-06"}, {"title": " 跳跃游戏---LeetCode45", "url": "./algorithms/LeetCode/LeetCode45.html", "date": "2020-05-04"}, {"title": " 旅行终点站---LeetCode5400", "url": "./algorithms/LeetCode/LeetCode5400.html", "date": "2020-05-03"}, {"title": " 绝对值差不超过限制的最长连续子数组---LeetCode5402", "url": "./algorithms/LeetCode/LeetCode5402.html", "date": "2020-05-03"}, {"title": " 无重复最长子串---LeetCode03", "url": "./algorithms/LeetCode/LeetCode03.html", "date": "2020-05-02"}, {"title": " 快乐数---LeetCode202判断链表环", "url": "./algorithms/LeetCode/LeetCode202.html", "date": "2020-04-30"}, {"title": " 山顶数组中查找目标值(二分法) --LeetCode1095", "url": "./algorithms/LeetCode/LeetCode1095.html", "date": "2020-04-29"}, {"title": " 使用xor来找只出现了一次的数字---LeetCode-m56", "url": "./algorithms/LeetCode/LeetCode-m56.html", "date": "2020-04-28"}, {"title": " 可获得最大点数(乱用DP=炸内存)", "url": "./algorithms/LeetCode/LeetCode5393.html", "date": "2020-04-26"}, {"title": " 合并K个排序链表", "url": "./algorithms/LeetCode/LeetCode23.html", "date": "2020-04-26"}, {"title": " 对角线遍历---内存开到爆怎么办?用vector吧", "url": "./algorithms/LeetCode/LeetCode5394.html", "date": "2020-04-26"}, {"title": " 逆序对", "url": "./algorithms/LeetCode/LeetCode-jz51.html", "date": "2020-04-24"}, {"title": " Leetcode_coins", "url": "./algorithms/LeetCode/LeetCode-coins.html", "date": "2020-04-23"}, {"title": " LeetCode05", "url": "./algorithms/LeetCode/LeetCode05.html", "date": "2020-04-23"}, {"title": " Leetcode445 两数相加(Stack)", "url": "./algorithms/LeetCode/Leetcode445.html", "date": "2020-04-22"}, {"title": " Leetcode199 二叉树右视图(DFS)", "url": "./algorithms/LeetCode/Leetcode199.html", "date": "2020-04-22"}]}
\ No newline at end of file
diff --git a/algorithms/AtCoder/README.md b/algorithms/AtCoder/README.md
deleted file mode 100644
index cf7cf06..0000000
--- a/algorithms/AtCoder/README.md
+++ /dev/null
@@ -1 +0,0 @@
-整理codeforces的算法题
\ No newline at end of file
diff --git a/algorithms/AtCoder/abc325_e.md b/algorithms/AtCoder/abc325_e.md
deleted file mode 100644
index f7508c1..0000000
--- a/algorithms/AtCoder/abc325_e.md
+++ /dev/null
@@ -1,120 +0,0 @@
----
-title: Dijkstra最短路,以及2N节点
-date: 2023-10-23 21:01:45
-tags: [最短路, dijkstra]
----
-# Dijkstra最短路,以及2N节点
-> 日期: 2023-10-23
-
-## 题目描述
-
-[E - Our clients, please wait a moment (atcoder.jp)](https://atcoder.jp/contests/abc325/tasks/abc325_e)
-
-## 示例
-
-```
-4 8 5 13
-0 6 2 15
-6 0 3 5
-2 3 0 13
-15 5 13 0
-
-78
-```
-
-
-
-## 解题思路
-
-第一次做atcoder,感觉还是有点难的,因为对最短路不熟悉,所以这道题完全没有意识到是最短路,因此在这里复习一下。
-
-总的来说,单源Djikstra最短路就是不停地寻找一个最近的一个没有vis过的节点(第一个while循环),去更新剩下的节点的dis(第二个while循环)。因为要挑选n个节点,所以最外层还有一个循环,所以复杂度是O(n^2)。
-
-这里给出一般的Dijkstra的写法:
-
-```cpp
-for(int t =0; t
dis[x] + grid[j][x]){
- dis[j] = dis[x] + grid[j][x];
- }
- }
- }
-```
-
-回到这道题,这道题虽然只有n个城市,但是在求最短路的时候,需要把它构造为有2n个点,来分别表示car的点和train的点,同时car的点可以走向train的点,但是trian的点不能走向car的点。
-
-这道题还有一点很妙的是,虽然我们构造出了一个2n的图,但是没有必要显示地把这个2n的图用邻接矩阵表示出来,只需要稍微处理一下,就用原来那个n*n的领结矩阵也是可以的(妙蛙)
-
-代码如下(参考了jiangly的代码,tql):
-
-```cpp
-#include
-using namespace std;
-
-using ll = long long;
-
-int main(){
- int n,a,b,c;;
- cin>>n>>a>>b>>c;
- vector> grid(n ,vector(n));
- for(int i=0;i> grid[i][j];
- }
- }
- vector dis(2*n, -1);
- vector vis(2*n, 0);
- dis[0] = 0;
- for(int t =0; t<2*n; t++){
- // 未选取的dis最小的点
- int x = -1;
- for(int i=0;i<2*n;i++){
- if(!vis[i] && dis[i] != -1 && (x == -1 || dis[i] < dis[x])){
- x = i;
- }
- }
- // 更新距离
- vis[x] = 1;
- if(x % 2 == 0){ // car
- // car到train的转移单独处理
- if(dis[x+1] == -1 || dis[x+1] > dis[x]){
- dis[x+1] = dis[x];
- }
- }
- for(int j=0; jcar train -> train
- ll v = dis[x];
- if(x % 2 == 0){
- v += grid[x/2][j] * a; // car
- }else{
- v += grid[x/2][j] * b + c; // train
- }
- if(dis[k] == -1 || dis[k] > v){
- dis[k] = v;
- }
- }
- }
-
- cout< 日期: 2023-10-11
-
-## 题目描述
-
-遇到了一个场景,差不多就是对于一个字符串,每一次删除其中一个元素,要使得删除后的字符串的字典序最小。
-
-然后把这些字符串拼在一起,给定一个pos,输出pos位置对应的字符。
-
-## 解题思路
-
-最开始想错了,以为是删除字符串里面最大的元素,其实不是,应该是删除字符串里面最靠前的一个元素,并且这个元素满足当前元素值比下一个元素大。
-
-比如说 cdea,那么顺序应该是先删除e,再删除d,再删除c,最后删除a。
-
-这满足一个单调栈的结构,所以这里使用了一个单调栈来做。
-
-大致就是这样的一个思路
-
-```c++
-int n = s.size();
-vector order(n, 0);
-stack st;
-int idx = 0;
-for(int i=0;i s[i]){
- order[st.top()] = idx;
- idx += 1;
- st.pop();
- }
- st.push(i);
-}
-while(!st.empty()){
- order[st.top()] = idx;
- idx += 1;
- st.pop();
-}
-```
-
-
-
-确定了删除顺序后,后面要找第pos个位置的字符就很简单了,先找到属于第几次删除后的结果,然后把这个结果算出来,最后找到就行了。
-
-```cpp
-#include
-using namespace std;
-int main(){
- int t;
- cin >> t;
- while(t--){
- string s;
- cin >> s;
- long long pos;
- cin >> pos;
- // 确定一个删除顺序
- int n = s.size();
- vector order(n, 0);
- stack st;
- int idx = 0;
- for(int i=0;i s[i]){
- order[st.top()] = idx;
- idx += 1;
- st.pop();
- }
- st.push(i);
- }
- while(!st.empty()){
- order[st.top()] = idx;
- idx += 1;
- st.pop();
- }
- // 查找pos来自于第几个序列
- long long sequenceIdx = 0;
- long long curLen = n;
- while(1){
- if(pos - curLen <= 0){
- break;
- }else{
- sequenceIdx += 1;
- pos -= curLen;
- curLen -= 1;
- }
- }
- // 构建出答案
- string tmp = "";
- for(int i=0;i= sequenceIdx){
- tmp += s[i];
- }
- }
-
- cout<
-### 第一题
-签到题。
-### 第二题
-第二题真的,我就是优化的方向错了。
-本来就是一个On²的嘛,然后呢,排序后早一点break我以为能过,不行。
-然后我就想到的上次用的那个map来存,我以为是重复数字太多了,然后试了一下,不行。
-然后换成两个map,不行。
-然后心态崩了,不知道该怎么优化。
-后来看了一下题解,怎么说呢,就是先对两个数组排序,然后一个正向遍历,一个反向遍历,这样两个数组都只走一遍就行了。(不得不说,看起来很简单,但是我真的没想到,也从来没有这么写过,真的学到了)。
-```cpp
-class Solution {
-public:
- int MOD = 1e9+7;
- int breakfastNumber(vector& staple, vector& drinks, int x) {
- int ans = 0;
- sort(staple.begin(),staple.end());
- sort(drinks.begin(),drinks.end());
- int pt = drinks.size()-1;
- for(int a:staple){
- while( pt>=0 && a + drinks[pt] > x ){
- pt--;
- }
- ans += pt+1;
- ans %= MOD;
- }
- return ans%MOD;
- }
-};
-```
-
-### 第三题
-第三题我真的想了好久。最后大体思路对了,但还是差一点,可惜了。
-心路历程如下:这道题是个啥,好难->果然还是要dp->长度1e5开不了二维dp->果然还是要贪心->不会贪->咦,可以开一维dp->思考了好久怎么一维dp->居然用上了前缀和和后缀和->走上了不归路
-说一下这道题的解法吧,就是可以这么想:
-ryr[i]表示从0到index i变成红黄红的最小次数。
-ry[i]表示i从0到index i变成红黄的最小次数。
-r[i]表示从i到index i变成红的最最小次数
-ryr(红黄红)是由ry或者ryr转移过来的(其实这个我写的时候并不是很确定,只能说是大胆猜想吧,稍微想一想好像还是没毛病),然后就可以开始dp了。
-同理ry是由ry或者r转移过来的(我当时就是没想到这一点,然后转而去直接计算ry,就是通过前缀和和后缀和来统计一个字符串前面的y数量和后部分的r数量,呃呃呃呃,复杂度直接就On²了,直接导致了超时)
-
-贴一发raw代码,这个思路大概是对了,但是超时了。
-```cpp
-class Solution {
-public:
- int INF = 9999999;
- int minimumOperations(string leaves) {
- //单侧dp即可
- int ry[100010];
- int ryr[100010];
- int prey[100010];
- int sufr[100010];
- memset(prey,0,sizeof(prey));
- memset(sufr,0,sizeof(sufr));
-
-
- //ry感觉不是推出来的,是算出来的
- int len = leaves.size();
- prey[0] = (leaves[0] == 'y');
- for(int i=1;i=0;i--){
- sufr[i] = (leaves[i] == 'r') + sufr[i+1];
- }
- for(int i=0;i=2){
- ry[i] = ry[i-1];
- }
- else{
- for(int k=0;k 日期: 2022-09-24
-
-去年的秋季编程大赛没有打,今年尝试参加了一下,跟两年前一样,三题飘过捏。
-### 第一题
-签到题
-### 第二题
-其实一点都不难,但是我读题没读清楚,一来就以为要求间接到达的路径,还在那用BFS搞了半天,最后发现题目要求的是直接到达,呵呵。。。
-### 第三题
-模拟题,没有啥难度,直接嗯写就行,稍微需要注意一下的就是棋盘往下走是+1不是-1哇,反正好像挺简单的。。。
-### 第四题
-真不会了,搞不定。
-
-### 总结
-重在参与。
-
-### 链接
-[题目链接](https://leetcode.cn/contest/season/2022-fall/?utm_campaign=contest_2022_fall_lccup&utm_medium=leetcode&utm_source=lc_navbar)
-
diff --git a/algorithms/LeetCode/LeetCode-LCP13.md b/algorithms/LeetCode/LeetCode-LCP13.md
deleted file mode 100644
index c619adb..0000000
--- a/algorithms/LeetCode/LeetCode-LCP13.md
+++ /dev/null
@@ -1,205 +0,0 @@
----
-title: 寻宝---LCP13(bfs+状压dp)
-date: 2020-07-29 16:49:32
-tags: [dp,动态规划,bfs,状态压缩]
----
-## 题目描述:
-我们得到了一副藏宝图,藏宝图显示,在一个迷宫中存在着未被世人发现的宝藏。
-迷宫是一个二维矩阵,用一个字符串数组表示。它标识了唯一的入口(用 'S' 表示),和唯一的宝藏地点(用 'T' 表示)。但是,宝藏被一些隐蔽的机关保护了起来。在地图上有若干个机关点(用 'M' 表示),只有所有机关均被触发,才可以拿到宝藏。
-要保持机关的触发,需要把一个重石放在上面。迷宫中有若干个石堆(用 'O' 表示),每个石堆都有无限个足够触发机关的重石。但是由于石头太重,我们一次只能搬一个石头到指定地点。
-迷宫中同样有一些墙壁(用 '#' 表示),我们不能走入墙壁。剩余的都是可随意通行的点(用 '.' 表示)。石堆、机关、起点和终点(无论是否能拿到宝藏)也是可以通行的。
-我们每步可以选择向上/向下/向左/向右移动一格,并且不能移出迷宫。搬起石头和放下石头不算步数。那么,从起点开始,我们最少需要多少步才能最后拿到宝藏呢?如果无法拿到宝藏,返回 -1 。
-
-## 示例:
-```cpp
-输入: ["S#O", "M..", "M.T"]
-输出:16
-
-解释:最优路线为: S->O, cost = 4, 去搬石头 O->第二行的M, cost = 3, M机关触发 第二行的M->O, cost = 3, 我们需要继续回去 O 搬石头。 O->第三行的M, cost = 4, 此时所有机关均触发 第三行的M->T, cost = 2,去T点拿宝藏。 总步数为16。
-```
-
-
-## 解题思路:
-一杯水,一包烟,一道dp写一天。
-这道题真神了,我记得当初春季大赛我第一看到就果断放弃,今天又看到这道题作为每日一题,心想着还是做一做,然后就做了一天23333。
-这道题主要有两个比较重要的点,一个是如何对数据进行预处理,一个是如何dp。
-先说如何对数据进行预处理吧,这道题的一个过程可以看作是从一个机关->石头->另一个机关这种方式在走,所以我们需要**先求出所有机关到所有石头的距离**(通过对每一个机关bfs来做),为了方便计算,我们把开始点也当作一个机关。同时还要计算所有机关到终点的距离。
-然而要进行上面的操作,我们要**先找到所有的机关和石头**,所以先要进行一次全局的bfs来找这些东西,还要找开始位置和终点。
-在进行了所有的这些操作后,还没完,我们还要**预先把机关到机关的距离求出来**,因为这道题虽然说是从机关->石头->机关,但本质上可以看作是机关之间的跳转,所以还要算一算机关之间的最小距离(也就是说,从一个机关到另一个机关经过哪块石头距离最小),把这些都算完了,才算预处理结束。(真的,NB)。
-然后我们就可以开始dp了,dp的式子是这样的dp[20][1<<17],**dp[i][j]表示以j为机关序列,最后一个处理的机关是i**,比如dp[1][3]就是序列为11的机关,最后一个处理的是index为1的机关。
-然后可以列出状态转移方程 **dp[i][state] = min(dp[j][state-(1<& maze) {
- //先找到所有的石头和机关
- //因为是100*100 所以没有必要构建结构体,直接把用x<<10 + y来表示坐标
- int xlen = maze.size();
- int ylen = maze[0].size();
- vector stones;
- vector triggers;
- int start;
- int target;
- queue q;
- node n;
- n.x = 0;
- n.y = 0;
- q.push(n);
- int vis[101][101]; memset(vis,0,sizeof(vis));
- vis[0][0] =1;
- while(!q.empty()){
- node curNode = q.front();
- q.pop();
- if(maze[curNode.x][curNode.y] == 'O') stones.push_back((curNode.x << 10) + curNode.y);
- if(maze[curNode.x][curNode.y] == 'M') triggers.push_back((curNode.x << 10) + curNode.y);
- if(maze[curNode.x][curNode.y] == 'S') start = (curNode.x<<10)+curNode.y;
- if(maze[curNode.x][curNode.y] == 'T') target = (curNode.x<<10)+curNode.y;
- //vis[curNode.x][curNode.y] = 1;
- for(int i=0;i<4;i++){
- int x = togo[i][0] + curNode.x;
- int y = togo[i][1] + curNode.y;
- if(x>=0 && x=0 && y>10;
- start.y = triggers[i]&1023;
- start.dis = 0;
- queue q;
- q.push(start);
- memset(vis,0,sizeof(vis));
- vis[start.x][start.y] = 1;
- while(!q.empty()){
- node2 curNode = q.front();
- q.pop();
- int x = curNode.x;
- int y = curNode.y;
- int curDis = curNode.dis;
- if(maze[x][y] == '#') continue; //遇到石头终止
- if(maze[x][y] == 'T') disToEnd[i] = curDis;
- if(maze[x][y] == 'O'){
- for(int j=0;j=0 && tox < xlen && toy >=0 && toy 日期: 2023-03-07
-
-## 题目描述
-
-「力扣嘉年华」的中心广场放置了一个巨型的二叉树形状的装饰树。每个节点上均有一盏灯和三个开关。节点值为 0 表示灯处于「关闭」状态,节点值为 1 表示灯处于「开启」状态。每个节点上的三个开关各自功能如下:
-
-开关 1:切换当前节点的灯的状态;
-开关 2:切换 以当前节点为根 的子树中,所有节点上的灯的状态,;
-开关 3:切换 当前节点及其左右子节点(若存在的话) 上的灯的状态;
-给定该装饰的初始状态 root,请返回最少需要操作多少次开关,可以关闭所有节点的灯。
-
-
-
-## 示例
-
-```
-输入:root = [1,1,0,null,null,null,1]
-输出:2
-```
-
-```
-输入:root = [1,1,1,1,null,null,1]
-输出:1
-```
-
-
-
-## 解题思路
-
-状态为: 节点, 该节点往前用的开关2是否为偶数, 该节点的父节点是否用了开关3
-
-这道题是树形dp,可以选择把dfs的返回值弄成一个长度为4的向量来标识4种状态的答案,但是这样弄递推公式写出来太容易出错了。
-
-所以我用了记忆化搜索的方式来写,但是使用记忆化搜索有一个问题,就是这里的状态中的一个维度是二叉树节点,也就是说会用到地址来作为第一维,所以一般的dp数据开得很难受,所以这里是用了一个unordered_map,这种方式还是第一次开。(PS:可以考虑遍历二叉树来为每一个节点赋予一个编号,那么就可以用一般的dp来开了)。
-
-这种unordered_map的方式太过于奇葩,所以不知道以后写树形dp是不是还要用这种方式。。。
-
-```c++
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-
-class Solution {
-public:
- //记忆化搜索
- unordered_map dp;
- int dfs(TreeNode* root, int switch2_odd, int switch3){
- if(root == nullptr) return 0;
- if(dp.count(root) > 0 && dp[root][switch2_odd][switch3] != -1){
- return dp[root][switch2_odd][switch3];
- }
-
- if(!dp.count(root))
- {
- memset(dp[root],-1,sizeof(dp[root]));
- }
- //灯为开,且 2 和 3 抵消,那么最后灯是开,要把灯关掉
- //选择奇数开关
- if( (root->val == 1) == (switch2_odd == switch3)){
- int res1 = dfs(root->left, switch2_odd, 0) + dfs(root->right, switch2_odd, 0) + 1;
- int res2 = dfs(root->left, !switch2_odd, 0) + dfs(root->right, !switch2_odd, 0) + 1;
- int res3 = dfs(root->left, switch2_odd, 1) + dfs(root->right, switch2_odd, 1) + 1;
- int res123 = dfs(root->left, !switch2_odd, 1) + dfs(root->right, !switch2_odd, 1) + 3;
- dp[root][switch2_odd][switch3] = min(min(min(res1,res2),res3),res123);
- }
- // 最后灯为关,要把灯关掉
- // 选择偶数开关或者不做操作
- else{
- int res = dfs(root->left, switch2_odd, 0) + dfs(root->right, switch2_odd, 0);
- int res12 = dfs(root->left, !switch2_odd, 0) + dfs(root->right, !switch2_odd, 0) + 2;
- int res13 = dfs(root->left, switch2_odd, 1) + dfs(root->right, switch2_odd, 1) + 2;
- int res23 = dfs(root->left, !switch2_odd, 1) + dfs(root->right, !switch2_odd, 1) + 2;
- dp[root][switch2_odd][switch3] = min(min(min(res,res12),res13),res23);
- }
-
- return dp[root][switch2_odd][switch3];
- }
-
- int closeLampInTree(TreeNode* root) {
- return dfs(root,0,0);
- }
-};
-```
-
-
-
-## 题目链接
-
-[LCP 64. 二叉树灯饰 - 力扣(LeetCode)](https://leetcode.cn/problems/U7WvvU/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode-coins.md b/algorithms/LeetCode/LeetCode-coins.md
deleted file mode 100644
index e661727..0000000
--- a/algorithms/LeetCode/LeetCode-coins.md
+++ /dev/null
@@ -1,62 +0,0 @@
----
-title: Leetcode_coins
-date: 2020-04-23 15:12:22
-tags: [dp, 背包问题]
----
-### 题目描述:
-硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007)
-
-### 示例:
-```cpp
-示例1:
-
- 输入: n = 5
- 输出:2
- 解释: 有两种方式可以凑成总金额:
-5=5
-5=1+1+1+1+1
-示例2:
-
- 输入: n = 10
- 输出:4
- 解释: 有四种方式可以凑成总金额:
-10=10
-10=5+5
-10=5+1+1+1+1+1
-10=1+1+1+1+1+1+1+1+1+1
-说明:
-
-注意:
-
-你可以假设:
-
-0 <= n (总金额) <= 1000000
-```
-
-### 解题思路:
-一下就能看出来是dp,要注意的是两层循环应该谁写外面。
-最开始写的是 1~n的循环在外面,然后每一层循环里分别取不同的硬币来相加,但是这样有可能会重复,比如当n=6时,选硬币1 + dp[5] 和 选硬币5 + dp[1] 是包含重复结果的,因为dp[5]中已经包含了硬币5这一种情况。
-解决方法就是在选硬币1时,不要去考虑更高面值的硬币,实际就是把两层循环换一下即可(妙啊)。
-
-```cpp
-class Solution {
-public:
- int waysToChange(int n) {
- int dp[1000001];//dp[i]表示当钱为i是的选择数
- memset(dp,0,sizeof(dp));
- int coins[4] = {1,5,10,25};
- dp[0]=1;
- for(int i=0;i<4;i++)
- {
- for(int j=coins[i];j<=n;j++)
- {
- dp[j] = (dp[j] + dp[j-coins[i]]) %1000000007 ;
- }
- }
- return dp[n];
- }
-};
-```
-
-### 题目链接:
-https://leetcode-cn.com/problems/coin-lcci/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode-jz11.md b/algorithms/LeetCode/LeetCode-jz11.md
deleted file mode 100644
index 3041752..0000000
--- a/algorithms/LeetCode/LeetCode-jz11.md
+++ /dev/null
@@ -1,75 +0,0 @@
----
-title: 剑指 Offer 11. 旋转数组的最小数字---(二分)
-date: 2020-07-22 10:43:17
-tags: [二分]
----
-## 题目描述:
-把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个递增排序的数组的一个旋转,输出旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一个旋转,该数组的最小值为1。
-
-## 示例:
-```cpp
-示例 1:
-输入:[3,4,5,1,2]
-输出:1
-
-示例 2:
-输入:[2,2,2,0,1]
-输出:0
-```
-
-
-## 解题思路:
-### 暴力遍历
-这不是遍历一下就完事了嘛,有什么好说的,其实也并不慢,都是O(n)了。
-
-```cpp
-class Solution {
-public:
- int minArray(vector& numbers) {
- int len = numbers.size();
- if(len == 1) return numbers[0];
- for(int i=1;i& numbers){
- if( l == r) return numbers[l];
-
- if(r-l == 1){
- if(numbers[l] < numbers[r]) return numbers[l];
- else return numbers[r];
- }
-
- if(numbers[l] >= numbers[r]){
- //左边的值比右边的大,说明旋转点在其中
- int mid = (l+r)/2;
- return min(binarySearch(l,mid,numbers),binarySearch(mid,r,numbers));
- }else{
- //旋转点不在其中
- return numbers[l];
- }
- return numbers[l];
- }
-
- int minArray(vector& numbers) {
- return binarySearch(0,numbers.size()-1,numbers);
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode-jz51.md b/algorithms/LeetCode/LeetCode-jz51.md
deleted file mode 100644
index e82e48a..0000000
--- a/algorithms/LeetCode/LeetCode-jz51.md
+++ /dev/null
@@ -1,185 +0,0 @@
----
-title: 逆序对
-date: 2020-04-24 20:30:04
-tags: [树状数组, bit, 归并排序, MergeSort, 逆序对, 二分查找, 离散化]
----
-### 题目描述:
-在数组中的两个数字,如果前面一个数字大于后面的数字,则这两个数字组成一个逆序对。输入一个数组,求出这个数组中的逆序对的总数。
-
-### 示例:
-```cpp
-示例 1:
-输入: [7,5,6,4]
-输出: 5
-```
-
-### 解题思路:
-这道题用了两种解法,归并排序和树状数组
-
-### 归并排序
-看题解之前完全没想到可以用归并排序来做,看了过后发现这么做简直太妙了。
-总之就是在归并排序的并阶段来计算逆序对,维护一个变量叫做currentAdd,用来保存当前要并的右半部分已经处理过的个数,也就是说,左边还没有加入的,每当加入,逆序对就会增加currentAdd这么多
-顺便还复习了一下归并排序,总之就是,先直接调归并来将左右两边先排好,然后再将这一次的来并起来,并好后,要把并好的结果赋给原数组。
-
-
-```cpp
-class Solution {
-public:
- int MergeSort(int l, int r, vector& nums)
- {
- if(r-l == 0)
- {
- return 0;
- }
- //先求左右两边中先求出来的逆序对
- int middle = (l+r)/2;
- int reversePairNum = MergeSort(l,middle,nums) + MergeSort(middle+1,r,nums);
- //当左右两边的nums都排好序了,可以计算组合时产生的逆序对
- vector temp;
- int lPointer = l;
- int rPointer = middle+1;
- int currentAdd = 0;
- while(!(lPointer>middle && rPointer>r))
- {
- if(lPointer > middle)
- {
- temp.push_back(nums[rPointer]);
- rPointer ++;
- }
- else if(rPointer > r)
- {
- reversePairNum += currentAdd;
- temp.push_back(nums[lPointer]);
- lPointer++;
- }
- else
- {
- if(nums[lPointer] > nums[rPointer] )
- {
- currentAdd++;
- temp.push_back(nums[rPointer]);
- rPointer++;
- }
- else
- {
- reversePairNum += currentAdd;
- temp.push_back(nums[lPointer]);
- lPointer++;
- }
- }
-
- }
- //将num变成排序后的num
- for(int i=0;i& nums) {
- if(nums.size() == 0)
- return 0;
- return MergeSort(0,nums.size()-1,nums);
- }
-};
-
-```
-
-
-
-
-
-### 树状数组
-以为这辈子都见不到树状数组了,没想到过了一年多又见面了,不过这次没这么头疼了哈哈哈,不过树状数组这种方法真的太难想了,估计真的碰到这种题我也不会知道可以用树状数组来解,除非是赤裸裸的单点更新+区间查询
-就是一般的树状数组
-ps:我写的树状数组的update函数是 +=这个值,不是 =这个值,被坑惨了。
-如果要求逆序对的话,把数值的大小作为树状数组的下标就好了
-这样,对原数组从后向前update树状数组,且每次加入都求一下当前的sum,就可以了
-需要注意的是,直接这么搞不行,如果原数组中有特别大的数,或者负数,作为树状数组的下标不科学,所以需要对原数组做处理,即排序后,用排序后的位置来代替自己的数值来作为树状数组的下标,即用相对位置来代替数值,相对位置用二分查找来找(直接从头到尾遍历找还会超时)。
-
-```cpp
-class Solution {
-public:
- int c[50002];
- int lowbit(int x)
- {
- return x&(-x);
- }
-
- void update(int pos,int changeValue,int n) //单点修改
- {
- for(int i=pos;i<=n;i+=lowbit(i))
- {
- c[i] += changeValue;
- }
- }
-
- int sum(int pos) // 查询从 1~pos的值
- {
- int ans=0;
- for(int i=pos;i>=1;i-=lowbit(i))
- {
- ans += c[i];
- }
- return ans;
- }
-
-
- //一定要用二分查找,顺序查找会tle
- int binarySerach(int value, vector& nums)
- {
- //nums is a sorted array
- int length = nums.size();
- int left = 0;
- int right = length-1;
- int middle = (left+right)/2;
- while(left nums[middle])
- {
- left = middle +1;
- }
- else if (value < nums[middle])
- {
- right = middle;
- }
- else
- {
- return middle;
- }
- }
- if(nums[left] == value)
- {
- return left;
- }
- else
- return -1;
- }
-
- int reversePairs(vector& nums) {
-
- vector sortedNums = nums;
- //将nums排序并存为一个新的数组,数的大小就可以由位置来体现,解决了数为负数以及数很大的问题
- sort(sortedNums.begin(),sortedNums.end());
- memset(c,0,sizeof(c));
- int length = nums.size();
- int ans=0;
- for(int i=length-1;i>=0;i--)
- {
- int index = binarySerach(nums[i],sortedNums)+1; //这里加个1,防止为0
- ans += sum(index-1);
- update(index,1,50002); //艹啊,这里的第二个参数是增量,不是改变的量,debug了半天,晕
- }
- return ans;
- }
-};
-
-```
-
-
-
-### 题目链接:
-https://leetcode-cn.com/problems/shu-zu-zhong-de-ni-xu-dui-lcof/
-[一个讲树状数组很好的博客](https://blog.csdn.net/bestsort/article/details/80796531)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode-m56.md b/algorithms/LeetCode/LeetCode-m56.md
deleted file mode 100644
index 0039651..0000000
--- a/algorithms/LeetCode/LeetCode-m56.md
+++ /dev/null
@@ -1,110 +0,0 @@
----
-title: 使用xor来找只出现了一次的数字---LeetCode-m56
-date: 2020-04-28 17:16:40
-tags: [位运算, 亦或]
----
-### 题目描述:
-一个整型数组 nums 里除两个数字之外,其他数字都出现了两次。请写程序找出这两个只出现一次的数字。要求时间复杂度是O(n),空间复杂度是O(1)。
-
-
-### 示例:
-```cpp
-示例 1:
-
-输入:nums = [4,1,4,6]
-输出:[1,6] 或 [6,1]
-示例 2:
-
-输入:nums = [1,2,10,4,1,4,3,3]
-输出:[2,10] 或 [10,2]
-
-
-限制:
-
-2 <= nums <= 10000
-
-```
-
-### 解题思路:
-给两个解法,一个是排序后找只出现了一次的,还有一个是用亦或运算,其实应该还可以用哈希映射来做,但空间复杂度有点高。这道题和joma那个视频不是很像吗2333。
-
-### 排序后找只出现了一次的
-排序后如果出现了两次的会相邻,根据这个特性,遍历一次就可以找出只出现了一次的
-
-```cpp
-class Solution {
-public:
- vector singleNumbers(vector& nums) {
- sort(nums.begin(),nums.end());
- vector ans;
- for(int i=0;i
-
-
-### 采用xor来做
-只出现过一次的数字,可以通过亦或找出来,但是这里有两个数字,所以找出来的结果是两个结果的抑或,所以需要将两个结果分开,分成两组,然后分别亦或找出结果。而要区别这两个结果,这两个数可以通过亦或结果里的1来区分,这里取最低位的1。
-注意与运算和==运算的优先级,与要加括号。
-
-```cpp
-class Solution {
-public:
- int lowbit(int x)
- {
- return x&(-x);
- }
-
- vector singleNumbers(vector& nums) {
- vector ans;
- int xorResult = 0;
- int length = nums.size();
- for(int i=0;i
-## 第一题
-没啥好说的
-## 第二题
-咳咳,第二题我疯狂超时了五发,说一下我是怎么优化的
-第二题其实就是给你两个数组,然后让你看一看一个数组中的平方是不是等于另外一个数组中某两个数的乘积,如果是的话,就+1。
-看起来很简单吧,直接写就是on3,超时妥妥的,不过我还是交了一发。
-思考半天后,我想到了用map来进行优化,也就是我建了4个map,然后分别存自己的乘积,两数相乘,但是还是超时了,代码长这样。
-```cpp
-class Solution {
-public:
- int numTriplets(vector& nums1, vector& nums2) {
- //试一下四个map哈
- //这特么也能超时,我很好奇正解是什么
- map apf;
- map acc;
- map bpf;
- map bcc;
-
- int len1 = nums1.size();
- int len2 = nums2.size();
-
- for(int i=0;i& nums1, vector& nums2) {
- //试一下四个map哈
- //这特么也能超时,我很好奇正解是什么
- map apf;
- map acc;
- map bpf;
- map bcc;
-
- int len1 = nums1.size();
- int len2 = nums2.size();
-
- for(int i=0;i (long long)nums1[i]*(long long)nums1[i]) break;
- // if((long long)nums2[j]*(long long)nums2[k] == (long long)nums1[i]*(long long)nums1[i]) ans++;
- // }
- // }
- // }
- // for(int i=0;i (long long)nums2[i]*(long long)nums2[i]) break;
- // if((long long)nums1[j]*(long long)nums1[k] == (long long)nums2[i]*(long long)nums2[i]) ans++;
- // }
- // }
- // }
- //草居然过不了 还是要map
-
-
- return ans;
- }
-};
-```
-
-最后,当我看到大佬的做法后,我震惊了,也就是说,其实根本没有必要创建四个map,使用两个map分别保存自己的平方就行了,然后在算两数乘积时,直接和存好的map直接比较不就行了吗?
-嗯。。。是的,所以我这里犯了一个很经典的错误:**明明能够直接比,偏要存下来再来比**
-
-## 第三题
-ez
-## 第四题
-重新温习了并查集,其实也不难。
-这道题的描述自己去看题吧,这里说一下思路。
-要求删除最多的边数,我们有理由认为应该尽量少删公共边,而尽量去删A和B自己的边。
-倒过来,也就是尽量多加公共边,然后尽量少加A和B自己的边。
-具体做法是这样的:
-先对全部公共边做判定,如果一条边对应的两个节点是连通的,那么就没必要加。
-对公共边判定完后,再分别的 A 和 B自己来以类似方法判定。
-代码如下(写得很垃圾,代码重复度高而且好像还很慢,不过过了):
-```cpp
-class Solution {
-public:
- int pre[100010];
- int preA[100010];
- int preB[100010];
- int find(int k) //寻找k的根结点
- {
- if(pre[k]==k) return k;
- return pre[k]=find(pre[k]);
- }
-
- void merge(int a,int b) //合并集合
- {
- int t1=find(a); //找到a和b的根结点
- int t2=find(b);
- if(t1!=t2) pre[t1]=t2; //靠右,即把左边的集合变成右边的子集合
- }
- int findA(int k) //寻找k的根结点
- {
- if(preA[k]==k) return k;
- return preA[k]=findA(preA[k]);
- }
-
- void mergeA(int a,int b) //合并集合
- {
- int t1=findA(a); //找到a和b的根结点
- int t2=findA(b);
- if(t1!=t2) preA[t1]=t2; //靠右,即把左边的集合变成右边的子集合
- }
- int findB(int k) //寻找k的根结点
- {
- if(preB[k]==k) return k;
- return preB[k]=findB(preB[k]);
- }
-
- void mergeB(int a,int b) //合并集合
- {
- int t1=findB(a); //找到a和b的根结点
- int t2=findB(b);
- if(t1!=t2) preB[t1]=t2; //靠右,即把左边的集合变成右边的子集合
- }
- int maxNumEdgesToRemove(int n, vector>& edges) {
- int ans = 0; //最少需要的边数
- for(int i=1;i<=n;i++) pre[i]=i;
- //先对类型3做处理,然后分别对alice和bob做处理
- int len = edges.size();
- for(int i=0;i
-
-### 解题思路:
-这道题的解法很多,我在这里总结了四种解法,分别是暴力解法1,暴力解法2,滑动窗口解法,滑动窗口的优化解法
-
-### 暴力解法1
-暴力解法1是我最先想到的解法,方法是从头到尾进行一次遍历,对于每一个字符,往后查找直到有重复字符,使用的方法是用一个数组来记录(用map也行,这道题很多地方都可以用map,不过用数组比较方便,我就都是用的数组)。每次选择一个字符时,都要对数组进行初始化。
-缺点就是每次初始化比较耗时,同时时间复杂度是O(n²)。
-
-```cpp
-class Solution {
-public:
- int lengthOfLongestSubstring(string s) {
- int map[1000];
- int max =0;
- int ans = 0;
- memset(map,0,sizeof(map));
- int length = s.length();
- for(int i=0;i0)
- {
- break;
- }
- max++;
- map[s[j]]++;
- }
- if(max > ans)
- ans = max ;
- }
- return ans;
- }
-};
-```
-
-
-
-### 暴力解法2
-暴力解法2是对长度进行遍历,相当于是给定一个固定长度的窗口,然后向后移动,不过虽然在改变数组时修改值是只改变了前后两个值,但是再查找是否有重复时还是采用的遍历,感觉比第一个解法还暴力,最后果不其然的超时了,这是虚假的滑动窗口。
-```cpp
-class Solution {
-public:
- int lengthOfLongestSubstring(string s) {
- int length = s.length();
- int flag[1000];
- int ans = length;
- while(ans > 1)
- {
- memset(flag,0,sizeof(flag));
- int right = 1;
- for(int i=0;i 1)
- right=0;
- }
- if(right == 1)
- return ans;
- for(int i=1;i+ans<=length;i++)
- {
- right = 1;
- flag[s[i-1]]--;
- flag[s[i+ans-1]]++;
- for(int j=i;j 1)
- {
- right=0;
- break;
- }
- }
- if(right == 1)
- {
- return ans;
- }
- }
- ans--;
- }
- return ans;
- }
-};
-```
-
-
-
-### 滑动窗口
-滑动窗口也可以叫双指针法,大体的思想是:如果当前子串没有重复,那么就把右指针往右移动一个单位;如果当前子串有重复,那么就把左指针往右移动一个单位。这里采用的方法是,每次移动左指针或者右指针后,都遍历判断一下当前是否有重复。实际上也是虚假的滑动窗口。
-```cpp
-class Solution {
-public:
- int lengthOfLongestSubstring(string s) {
- int left =0;
- int right = 0;
- int length = s.length();
- bool isLongest = 1;
- int max = 1;
- int flag[200];
- if(length == 0)
- return 0;
- while( !( (right == (length-1)) && isLongest))
- {
- if(isLongest)
- {
- if(right-left+1 > max)
- max = right-left+1;
- right = (right+1 == length)?right:right+1;
- }
- else
- {
- left++;
- }
- memset(flag,0,sizeof(flag));
- isLongest = 1;
- for(int i=left;i<=right;i++)
- {
- flag[s[i]]++;
- if(flag[s[i]] > 1)
- {
- isLongest = 0;
- break;
- }
- }
- }
- return (right-left+1)>max?(right-left+1):max;
- }
-};
-```
-
-
-
-
-### 滑动窗口的优化
-既然使用了滑动窗口,那么实际上每次的遍历找是否重复是没有必要的,因为如果有重复,那么必然来自于最近一次右边的移动,而且肯定只会重复一次。根据这一特性,可以把重复的字符给保存下来,如果左边往右移动时将这一个字符给去掉了,那么当前就又是一个无重复子串。
-```cpp
-class Solution {
-public:
- int lengthOfLongestSubstring(string s) {
- //初始化
- int left =0;
- int right = 0;
- int length = s.length();
- bool isLongest = 1;
- int max = 1;
- int flag[200];
- memset(flag,0,sizeof(flag));
- flag[s[0]]++;
- int curDoubleLetter=-1;
- if(length == 0)
- return 0;
- while( !( (right == (length-1)) && isLongest))
- {
- if(isLongest)
- {
- if(right-left+1 > max)
- max = right-left+1;
- if(right +1 == length)
- {
- //nothing
- }
- else
- {
- right = right +1;
- flag[s[right]]++;
- if(flag[s[right]] >1)
- {
- isLongest = 0;
- curDoubleLetter = s[right];
- }
- }
-
- }
- else
- {
- left++;
- //cout<max?(right-left+1):max;
- }
-};
-```
-
-
-### 题目链接:
-https://leetcode-cn.com/problems/longest-substring-without-repeating-characters/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode04.md b/algorithms/LeetCode/LeetCode04.md
deleted file mode 100644
index 039f412..0000000
--- a/algorithms/LeetCode/LeetCode04.md
+++ /dev/null
@@ -1,115 +0,0 @@
----
-title: 寻找两个正序数组的中位数---LeetCode04(噩梦级边界判断)
-date: 2020-05-24 13:35:56
-tags: [二分]
----
-## 题目描述:
-给定两个大小为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。
-请你找出这两个正序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
-你可以假设 nums1 和 nums2 不会同时为空。
-
-## 示例:
-```cpp
-示例 1:
-nums1 = [1, 3]
-nums2 = [2]
-则中位数是 2.0
-
-示例 2:
-nums1 = [1, 2]
-nums2 = [3, 4]
-则中位数是 (2 + 3)/2 = 2.5
-```
-
-
-## 解题思路:
-这道题首先可以看到复杂度是O(log(m + n)),所以一般用的像归并,以及双指针的方法就不行了。这道题一看就是二分,但是一开始我也没看懂怎么二分,最后就直接看题解了。
-这道题首先要把问题进行一个转换,要找到中位数实际上就是要找到第k个数,这里的k是 (length1+length2+1)/2 和 (length1+length2+2)/2,这里之所以要取两个k是因为奇数个数的中位数和偶数个数的中位数可以通过这种方法来进行一个统一。在奇数的情况下,(length1+length2+1)/2和(length1+length2+2)/2是相同的,在偶数的情况下,(length1+length2+1)/2和(length1+length2+2)/2就是中间的那两个数。所以两个加起来除以2就是最终答案。
-知道了这道题的本质就是找到第k个数后,就可以开始二分了。这道题的二分非常巧妙,就是拿两个数组的第k/2个数进行比较,小的那个数组的第k/2个数以及前面的全部数都不可能是第k个数了,所以就把前面舍去(就是更新offset),然后更新k,最后就相当于两个新的数组,找到新的第k个数(递归)。(这里面涉及了非常多的边界判定,说不清楚了,具体的见注释吧。)
-
-```cpp
-class Solution {
-public:
- int findKSmallestNum(vector& nums1, vector& nums2, int offset1,int offset2,int k)
- {
- int length1 = nums1.size();
- int length2 = nums2.size();
- //如果数组为空,那么就直接返回
- if(offset1 >= length1)
- {
- return nums2[offset2+k-1];
- }
- if(offset2 >= length2)
- {
- return nums1[offset1+k-1];
- }
- //如果数组越界,取越界数组的最后一个元素来和另一个的k/2来比
- if(offset1 + k/2 -1 >= length1)
- {
- //如果越界的最后一个更小
- if(nums1[length1-1] < nums2[offset2 + k/2 -1])
- {
- k = k - (length1-offset1);
- return nums2[offset2+k-1];
- }
- else
- {
- offset2 += k/2;
- k -= k/2;
- return findKSmallestNum(nums1,nums2,offset1,offset2,k);
- }
- }
- if(offset2 + k/2 -1 >= length2)
- {
- if(nums2[length2-1] < nums1[offset1 + k/2 -1])
- {
- //如果越界的最后一个更小
- k = k - (length2-offset2);
- return nums1[offset1+k-1];
- }
- else
- {
- offset1 += k/2;
- k -= k/2;
- return findKSmallestNum(nums1,nums2,offset1,offset2,k);
- }
- }
- //如果k为1,直接返回两个数组的开头两个的最小的那个
- if(k==1) return min(nums1[offset1],nums2[offset2]);
- //比较两个数组的k/2
- if(nums1[k/2+offset1-1] < nums2[k/2+offset2-1])
- {
- //nums1前面都不是第k小
- offset1 += k/2;
- k -= k/2;
- }
- else
- {
- offset2 += k/2;
- k -= k/2;
- }
- return findKSmallestNum(nums1,nums2,offset1,offset2,k);
- }
-
- double findMedianSortedArrays(vector& nums1, vector& nums2) {
- //寻找第k小的数就是拿两个数组的k/2相比,小的那个数组的第k/2包括前面的都不可能是第k小的,然后把k -= k/2,再从新的数组开始找
- int length1 = nums1.size();
- int length2 = nums2.size();
- int offset1 = 0;
- int offset2 = 0;
- int k1 = (length1+length2+1) /2;
- int k2 = (length1+length2+2) /2;
- // cout<<"k1:"<=0; j++)
- {
- if(s[i-j] == s[i+j])
- {
- pre += s[i-j];
- back += s[i+j];
- }
- else
- {
- break;
- }
- }
-
- //pre需要reverse一下
- std::reverse(pre.begin(),pre.end());
- string tmpAns = pre + middle + back;
- int tmpLength = tmpAns.length();
- if(tmpLength > maxLength)
- {
- ans = tmpAns;
- maxLength = tmpLength;
- }
-
- }
- //把输出结果中的#去掉
- string realAns = "";
- for(int i=0;i
-
-
-
-### dp
-先初始化所有一回文和二回文的情况,然后再通过动态规划求出所有三回文直到length回文的情况
-递推公式 dp[i][j] = dp[i+1][j-1] ==1 && s[i]==s[j]
-注意两层循环,表示回文串长度的循环要放外面,不然就不对,因为这样可能在index为0时,会错过长度为4的回文,因为后面还没弄过。
-
-```cpp
-class Solution {
-public:
- string longestPalindrome(string s) {
- //dp法
- int start =0;
- int end =0;
- int dp[1000][1000]; //dp[i][j]==1代表在s中(i,j)位置的是一个回文字串
- memset(dp,0,sizeof(dp));
- //初始化所有一回文和二回文的情况
- int length = s.length();
- for(int i=0;i
-
-
-
-### 马拉车算法
-在这里贴一个讲马拉车讲的很好的B站视频:
-https://www.bilibili.com/video/BV1ft4y117a4
-
-马拉车算法和中心展开其实很像,只不过很好地利用了回文串的对称性来避免重复计算
-对字符串预处理是为了让全部都变成奇回文串的情况
-马拉车算法维护了一个最右回文子串,当对一个字符串从左到右进行遍历求d[i]时,如果i在最右回文子串中,就可以利用对称性来为d[i]初始化一个值,然后再中心展开,不然就直接中心展开。
-最后得出结果时,可以发现,最终的回文串长度就是d[i]-1,最终的最长回文串在原始字符串中的起始index,就是修改后字符串中,(d[i]最大的index - d[i])/2
-
-```cpp
-class Solution {
-public:
- struct tarStringInfo{
- int index; //最长回文子串的开始位置
- int length; //最长回文子串的长度
- };
-
- string preMake(string s)
- {
- //先对s做预处理
- string newS="@#";
- for(int i=0;i d; //d数组
- int length = s.length();
- d.push_back(0); //@对应位置的回文半径是0
- d.push_back(1); //第一个字符对应的回文半径必定是1
- right =1;
- middle =1;
- for(int i=2;i=1 && i+l < length-1 )
- {
- if(s[i+l] == s[i-l])
- {
- d[i]++;
- }
- l++;
- }
- if(d[i] > maxDis)
- {
- maxDis = d[i];
- maxIndex=i;
- }
- right = i + d[i] -1;
- middle =i;
- }
-
- //对应回原字符串,回文长度就是d[i]-1,回文开始的位置就是 (index-d[i])/2
- tarStringInfo ans;
- ans.length = maxDis -1;
- ans.index = (maxIndex - maxDis)/2;
- return ans;
- }
-
- string longestPalindrome(string s) {
- tarStringInfo ans = Manacher(s);
- return s.substr(ans.index,ans.length);
- }
-};
-```
-
-### 题目链接:
-https://leetcode-cn.com/problems/longest-palindromic-substring/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode102.md b/algorithms/LeetCode/LeetCode102.md
deleted file mode 100644
index 6dc5f7c..0000000
--- a/algorithms/LeetCode/LeetCode102.md
+++ /dev/null
@@ -1,132 +0,0 @@
----
-title: 二叉树层序遍历----LeetCode102
-date: 2020-05-13 21:04:39
-tags: [树, bfs]
----
-### 题目描述:
-给你一个二叉树,请你返回其按 层序遍历 得到的节点值。(即逐层地,从左到右访问所有节点)。
-
-### 示例:
-```cpp
-示例:
-二叉树:[3,9,20,null,null,15,7],
- 3
- / \
- 9 20
- / \
- 15 7
-返回其层次遍历结果:
-[
- [3],
- [9,20],
- [15,7]
-]
-```
-
-### 解题思路:
-昨天的题太水了,没更新,今天的稍微有一点写的价值吧(shuiyixia)。
-这里讲两个思路,一个是正常人做法(略微繁琐),另一个要稍微多想一步。
-
-### 方法一
-正常bfs,创建一个结构体,来记录level,然后bfs遍历过程中,把level对应的结果存下来,最后再整理输出,略微繁琐,因为要遍历两次。
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-
-struct myNode{
- TreeNode* node;
- int level;
-};
-
-class Solution {
-public:
- vector> levelOrder(TreeNode* root) {
- vector record[1000];
- vector> ans;
- for(int i=0;i<1000;i++) record[i].clear();
- queue q;
- myNode start;
- start.node = root;
- start.level = 0;
- q.push(start);
-
- while(!q.empty())
- {
- myNode temp = q.front();
- if(temp.node != NULL)
- {
- myNode newAdd;
- record[temp.level].push_back(temp.node->val);
- //push left node
- newAdd.node = temp.node->left;
- newAdd.level = temp.level+1;
- q.push(newAdd);
- //push right node
- newAdd.node = temp.node->right;
- newAdd.level = temp.level+1;
- q.push(newAdd);
- }
- q.pop();
- }
- for(int i=0;i<1000;i++)
- {
- if(record[i].size() == 0)
- break;
- vector temp;
- for(int j=0;j> levelOrder(TreeNode* root) {
- queue q;
- if(root != NULL)
- q.push(root);
- vector> ans;
- while(!q.empty())
- {
- int length = q.size();
- vector tempv;
- for(int j=0;jval);
- q.pop();
- if(temp->left != NULL) q.push(temp->left);
- if(temp->right != NULL) q.push(temp->right);
- }
- ans.push_back(tempv);
- }
- return ans;
- }
-};
-```
-
-### 题目链接:
-https://leetcode-cn.com/problems/binary-tree-level-order-traversal/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1025.md b/algorithms/LeetCode/LeetCode1025.md
deleted file mode 100644
index 74e0af6..0000000
--- a/algorithms/LeetCode/LeetCode1025.md
+++ /dev/null
@@ -1,51 +0,0 @@
----
-title: 除数博弈---LeetCode1025(智力题)
-date: 2020-07-24 10:06:17
-tags: [分析]
----
-## 题目描述:
-这里写题目描述爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
-最初,黑板上有一个数字 N 。在每个玩家的回合,玩家需要执行以下操作:
-
-选出任一 x,满足 0 < x < N 且 N % x == 0 。
-用 N - x 替换黑板上的数字 N 。
-如果玩家无法执行这些操作,就会输掉游戏。
-只有在爱丽丝在游戏中取得胜利时才返回 True,否则返回 false。假设两个玩家都以最佳状态参与游戏。
-
-## 示例:
-```cpp
-示例 1:
-输入:2
-输出:true
-解释:爱丽丝选择 1,鲍勃无法进行操作。
-
-示例 2:
-输入:3
-输出:false
-解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
-
-```
-
-## 解题思路:
-这道题看起来很唬人,其实就是一道找规律的题。
-随便列几项:
-1. 当alice先手为1,alice输
-2. 当alice先手为2,alice只能拿1,那么bob输
-3. 当alice先手为3,alice只能拿1,然后就成为了bob先手为2,所以alice输
-4. 当alice先手为4,alice可以拿1,2。如果alice拿1,成为bob先手为3,alice赢;如果alice拿2,成为bob先手2,alice输,所以alice只会去拿1。
-
-稍微观察一下容易发现规律(?),alice先手为奇数时,alice必输。因为奇数的因数只有奇数,所以bob拿到的一定是一个偶数,然后bob取的时候会选择给alice一个奇数,然后一直套娃,最后肯定是alice输。当alice先手为偶数时,同理,alice会选择给bob一个奇数,然后bob就凉了(这里解释一下,因为自己为偶数时,大多数情况下可以选择给别人一个偶数,也可以选择给别人一个奇数,当然,耍赖的情况下一直取1就行了,偶数-1一定是一个奇数)。
-
-找规律还是挺有意思的,这道题还可以用dp做,但好像没必要,就不想了。
-
-```cpp
-class Solution {
-public:
- bool divisorGame(int N) {
- return (N%2 == 0);
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/divisor-game/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1049.md b/algorithms/LeetCode/LeetCode1049.md
deleted file mode 100644
index ff5e2ec..0000000
--- a/algorithms/LeetCode/LeetCode1049.md
+++ /dev/null
@@ -1,78 +0,0 @@
----
-title: 最后一块石头的重量 II---(还是背包)
-date: 2023-02-15 21:55:48
-tags: [dp]
----
-# 最后一块石头的重量 II---(还是背包)
-> 日期: 2023-02-15
-
-## 题目描述
-
-有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
-
-每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
-
-如果 x == y,那么两块石头都会被完全粉碎;
-如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
-最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
-
-## 示例
-
-```
-输入:stones = [2,7,4,1,8,1]
-输出:1
-解释:
-组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
-组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
-组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
-组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
-
-```
-
-```
-输入:stones = [31,26,33,21,40]
-输出:5
-```
-
-
-
-## 解题思路
-
-这道题和[416. 分割等和子集 - 力扣(LeetCode)](https://leetcode.cn/problems/partition-equal-subset-sum/)差不多,稍微分析一下就会发现,这道题也是尽量把这堆石头分为相等的两份。
-
-```cpp
-class Solution {
-public:
- int lastStoneWeightII(vector& stones) {
- //感觉像是将石头分为尽可能均等的两份
- //[2,7,4,1,8,1] -> [2,8,1] [4,7,1]
- //[31,26,33,21,40] -> [21,26,31] [33,40]
- // 感觉和 https://leetcode.cn/problems/partition-equal-subset-sum/ 差不多
- int sum = 0;
- for(int x:stones){
- sum += x;
- }
- int target = sum/2;
- int dp[3090];
- for(int i=0;i<3090;i++) dp[i] = 0;
- for(int i=0;i=stones[i];j--){
- dp[j] = max(dp[j], dp[j-stones[i]] + stones[i]);
- }
- }
-
- return sum-dp[target]-dp[target];
-
- }
-};
-```
-
-这里再明确一下dp[i]的意义,它的意思是背包容量为i时的最大价值,因为这里价值就是重量,那么意思就是背包容量为i时的最大重量,也就是说dp[i]的值是不会比i大的。
-
-因为我们的目标是尽量对半分,所以最好的情况就是 dp[target] == target,如果不是的话,那么少的那一半的重量dp[target], 所以多的那一半就是 sum - dp[target],所以最后返回的结果是 (sum - dp[target]) - dp[target]。
-
-
-
-## 题目链接
-
-[1049. 最后一块石头的重量 II - 力扣(LeetCode)](https://leetcode.cn/problems/last-stone-weight-ii/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode105.md b/algorithms/LeetCode/LeetCode105.md
deleted file mode 100644
index 9e36144..0000000
--- a/algorithms/LeetCode/LeetCode105.md
+++ /dev/null
@@ -1,214 +0,0 @@
----
-title: 从前序与中序遍历序列构造二叉树---LeetCode105
-date: 2020-05-22 14:53:04
-tags: [递归, 树]
----
-### 题目描述:
-根据一棵树的前序遍历与中序遍历构造二叉树。
-注意:
-你可以假设树中没有重复的元素。
-
-### 示例:
-```cpp
-例如,给出
-前序遍历 preorder = [3,9,20,15,7]
-中序遍历 inorder = [9,3,15,20,7]
-
-返回如下的二叉树:
- 3
- / \
- 9 20
- / \
- 15 7
-
-```
-
-
-
-### 解题思路:
-这道题主要就是用递归的方法来做,先在中序遍历中找到根,然后就可以知道左子树和右子树的数量,然后就可以在前序遍历中找到左子树和右子树,根据新的左子树前序遍历和中序遍历 以及 右子树前序遍历和中序遍历,继续往下构建树,思想很简单,其实写起来还是有点复杂的。
-这道题还有一个迭代的做法,我有点没看懂,就不写了。
-
-### 优化前的递归
-优化前我是在每次递归时都去构建了新的vector来作为参数传下去,所以有点慢。
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-class Solution {
-public:
-
- void helper(vector& preorder, vector& inorder,TreeNode* root)
- {
- //前序遍历的第一个元素是根,通过在中序遍历中找到根可以判断出左子树和右子树的个数
- //根据左子树和右子树的个数可以在前序遍历中找到左儿子和右儿子
- int preLength = preorder.size();
- int inLength = inorder.size();
- //如果当前只有一个元素 或者说没有root,直接返回
- if(preLength == 1 || root==NULL) return;
- int cnt = 0;
- for(int i=0;ileft = NULL;
- else
- root->left = new TreeNode(preorder[1]);
-
- if( cnt+1 == inLength)
- root->right = NULL;
- else
- root->right = new TreeNode(preorder[1+cnt]);
-
- //构建新的left 和 right的vector
- vector leftPre;
- vector leftIn;
- vector rightPre;
- vector rightIn;
-
-
- int temp = 0;
- for(int i=1;ileft);
- helper(rightPre,rightIn,root->right);
- return;
- }
-
- TreeNode* buildTree(vector& preorder, vector& inorder) {
- if(preorder.size() == 0 ) return NULL;
- TreeNode* root = new TreeNode(preorder[0]);
- helper(preorder,inorder,root);
- return root;
- }
-};
-```
-
-
-
-### 优化后的递归
-但是其实不用每次都去构建vector,只需要把对应的左边和右边的index记录一下就可以了。
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-class Solution {
-public:
- vector preOrder;
- vector inOrder;
-
- void helper(TreeNode* root,int preLeftIndex,int preRightIndex,int inLeftIndex,int inRightIndex)
- {
- //在中序遍历中寻找root
- if(preRightIndex-preLeftIndex == 0 || root == NULL ) return;
- int cnt = 0;
- for(int i=inLeftIndex ;i<=inRightIndex;i++)
- {
- if(inOrder[i] != root->val)
- {
- cnt++;
- }
- else
- {
- break;
- }
- }
- //确定左子树和右子树的根
- if(cnt == 0)
- root->left = NULL;
- else
- root->left = new TreeNode(preOrder[preLeftIndex+1]);
-
- if(cnt +1 == inRightIndex-inLeftIndex +1) //如果cnt+1就是length
- root->right = NULL;
- else
- root->right = new TreeNode(preOrder[preLeftIndex+1+cnt]);
-
- //建立左子树和右子树
- helper(root->left,preLeftIndex+1,preLeftIndex+cnt,inLeftIndex,inLeftIndex+cnt-1);
- helper(root->right,preLeftIndex+cnt+1,preRightIndex,inLeftIndex+cnt+1,inRightIndex);
- }
-
- TreeNode* buildTree(vector& preorder, vector& inorder) {
- //存一下,递归懒得传参
- if(preorder.size() == 0 ) return NULL;
- preOrder = preorder;
- inOrder = inorder;
- TreeNode* root = new TreeNode(preOrder[0]);
- int length = preorder.size();
- helper(root,0,length-1,0,length-1);
- return root;
- }
-};
-```
-
-
-### 题目链接:
-https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode109.md b/algorithms/LeetCode/LeetCode109.md
deleted file mode 100644
index 5b95739..0000000
--- a/algorithms/LeetCode/LeetCode109.md
+++ /dev/null
@@ -1,98 +0,0 @@
----
-title: 有序链表转换二叉搜索树---LeetCode109
-date: 2020-08-18 14:23:47
-tags: [二叉搜索树, BST, 链表, 快慢指针]
----
-## 题目描述:
-给定一个单链表,其中的元素按升序排序,将其转换为高度平衡的二叉搜索树。
-本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。
-
-## 示例:
-```cpp
-这里放测试样例给定的有序链表: [-10, -3, 0, 5, 9],
-一个可能的答案是:[0, -3, 9, -10, null, 5], 它可以表示下面这个高度平衡二叉搜索树:
- 0
- / \
- -3 9
- / /
- -10 5
-
-```
-
-## 解题思路:
-思路有两个,一个是一直找中心点,一个是用中序遍历。
-### 找中心点
-想要得到一个平衡的二叉搜索树,最重要的就是如何选择二叉搜索树的根,很自然的想法就是一直选取中心点。
-选择中心点的方法有两种:
-1. 将链表转为数组,然后直接选。
-2. 使用快慢指针法,将两个指针都设置在头节点,然后同时开始走,慢指针每次走一格,快指针每次走两格,当快指针走到尾部,满指针刚好走到中间。(这个方法看起来很巧妙,但是在数据规模小的时候,还是转数组比较香)。
-```cpp
-class Solution {
-public:
- int num[100000];
-
- TreeNode* makeTree(int left,int right){
- if(left>right) return nullptr;
- if(left == right){
- return new TreeNode(num[left]);
- }
- int mid = (left+right)/2;
- TreeNode* midNode = new TreeNode(num[mid]);
- midNode->left = makeTree(left,mid-1);
- midNode->right = makeTree(mid+1,right);
- return midNode;
- }
-
- TreeNode* sortedListToBST(ListNode* head) {
- //先把链表转为数组
- TreeNode* ans = new TreeNode();
- int length = 0;
-
- memset(num,0,sizeof(num));
- while(head!=nullptr){
- num[length] = head->val;
- head = head->next;
- length++;
- }
- return makeTree(0,length-1);
- }
-};
-```
-
-### 中序遍历
-这个方法真的妙,要使用这个方法你首先要意识到对一个BST进行中序遍历得到的就是一个有序的序列,于是我们就可以反过来根据有序的序列来构建出这个BST。
-构建BST的过程也很妙,用到了一个全局的遍历链表的指针,然后每次在设置一个子树的root的值时,使用这个指针的val然后指针后移。这样就实现了遍历链表和建树的同步。
-```cpp
-class Solution {
-public:
- ListNode* curNode;
- TreeNode* buildBST(int left,int right){
- if(left > right) return nullptr;
- int mid = (left+right)/2;
- //先建立左子树
- TreeNode* leftSubTree = buildBST(left,mid-1);
- TreeNode* root = new TreeNode(curNode->val);
- curNode = curNode->next;
- TreeNode* rightSubTree = buildBST(mid+1,right);
- root->left = leftSubTree;
- root->right = rightSubTree;
- return root;
- }
-
- TreeNode* sortedListToBST(ListNode* head) {
- //搞一个全局的指针来遍历链表
- //然后中序遍历填值,这样遍历链表和建树就是同步的
- ListNode* cur = head;
- int len = 0;
- while(cur!=nullptr){
- len++;
- cur = cur->next;
- }
- curNode = head;
- return buildBST(0,len-1);
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/convert-sorted-list-to-binary-search-tree/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1095.md b/algorithms/LeetCode/LeetCode1095.md
deleted file mode 100644
index f19cc80..0000000
--- a/algorithms/LeetCode/LeetCode1095.md
+++ /dev/null
@@ -1,181 +0,0 @@
----
-title: 山顶数组中查找目标值(二分法) --LeetCode1095
-date: 2020-04-29 17:14:45
-tags: [二分, BinarySerach]
----
-## 题目描述:
-(这是一个 交互式问题 )
-
-给你一个 山脉数组 mountainArr,请你返回能够使得 mountainArr.get(index) 等于 target 最小 的下标 index 值。
-
-如果不存在这样的下标 index,就请返回 -1。
-
-
-
-何为山脉数组?如果数组 A 是一个山脉数组的话,那它满足如下条件:
-
-首先,A.length >= 3
-
-其次,在 0 < i < A.length - 1 条件下,存在 i 使得:
-
-A[0] < A[1] < ... A[i-1] < A[i]
-A[i] > A[i+1] > ... > A[A.length - 1]
-
-
-你将 不能直接访问该山脉数组,必须通过 MountainArray 接口来获取数据:
-
-MountainArray.get(k) - 会返回数组中索引为k 的元素(下标从 0 开始)
-MountainArray.length() - 会返回该数组的长度
-
-
-注意:
-
-对 MountainArray.get 发起超过 100 次调用的提交将被视为错误答案。此外,任何试图规避判题系统的解决方案都将会导致比赛资格被取消。
-
-为了帮助大家更好地理解交互式问题,我们准备了一个样例 “答案”:https://leetcode-cn.com/playground/RKhe3ave,请注意这 不是一个正确答案。
-
-### 示例:
-```cpp
-示例 1:
-
-输入:array = [1,2,3,4,5,3,1], target = 3
-输出:2
-解释:3 在数组中出现了两次,下标分别为 2 和 5,我们返回最小的下标 2。
-示例 2:
-
-输入:array = [0,1,2,4,2,1], target = 3
-输出:-1
-解释:3 在数组中没有出现,返回 -1。
-
-
-提示:
-
-3 <= mountain_arr.length() <= 10000
-0 <= target <= 10^9
-0 <= mountain_arr.get(index) <= 10^9
-
-来源:力扣(LeetCode)
-链接:https://leetcode-cn.com/problems/find-in-mountain-array
-著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-```
-
-### 解题思路:
-这道题不能直接从头到尾遍历,因为题目说请求index的数据过多会报错,所以明显只能二分。
-先通过二分找出山顶位置,然后在山顶位置前二分找出第一个答案,山顶位置后找出第二个答案就可以了。
-注意山顶前的排序是从小到大,山顶后的排序是从大到小,两个的二分是反着来的。
-
-```cpp
-/**
- * // This is the MountainArray's API interface.
- * // You should not implement it, or speculate about its implementation
- * class MountainArray {
- * public:
- * int get(int index);
- * int length();
- * };
- */
-
-int binarySerach(MountainArray &mountainArr, int target, int start, int end)
-{
- int left = start;
- int right = end;
- int middle = 0;
- while(left <= right)
- {
- middle = (left+right) /2;
- if(mountainArr.get(middle) == target)
- return middle;
- if(target < mountainArr.get(middle))
- {
- right = middle -1;
- }
- else
- {
- left = middle+1;
- }
- }
- return -1;
-}
-
-int reverseBinarySerach(MountainArray &mountainArr, int target, int start, int end)
-{
- int left = start;
- int right = end;
- int middle = 0;
- while(left <= right)
- {
- middle = (left+right) /2;
- if(mountainArr.get(middle) == target)
- return middle;
- if(target < mountainArr.get(middle))
- {
- left = middle+1;
- }
- else
- {
- right = middle -1;
- }
- }
- return -1;
-}
-
-
-
-
-class Solution {
-public:
- int findInMountainArray(int target, MountainArray &mountainArr) {
- int length = mountainArr.length();
- //find moutain top
- int left = 1; //山顶不会出现在0或者length-1
- int right = length -2;
- int middle = 0;
- int moutainTopIndex = 0;
- while(1)
- {
- //left =1 right = 2 middle = 1
- middle = (left+right)/2;
- //山顶不会出现在0或者length-1
- int curLeft = mountainArr.get(middle-1);
- int cur = mountainArr.get(middle);
- int curRight = mountainArr.get(middle+1);
- if(cur > curLeft && cur > curRight)
- {
- moutainTopIndex = middle;
- break;
- }
- else if(curLeft < cur && cur < curRight)
- {
- //左边山
- left = middle +1;
- }
- else if(curLeft > cur && cur > curRight)
- {
- ///右边山
- right = middle -1;
- }
- }
- cout<<"length: "< 日期: 2022-09-28
-
-## 题目描述
-
-给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
-
-找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
-
-返回容器可以储存的最大水量。
-
-说明:你不能倾斜容器。
-
-## 示例
-
-```
-输入:[1,8,6,2,5,4,8,3,7]
-输出:49
-解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
-
-```
-
-
-
- -
-
-
-## 解题思路
-
-这道题是贪心,用两个位置来表示区间,并且判断左右两边的大小,并且移动小的那一边。
-
-这个方法很好想,好像可以通过反证法去证明它不是错的。。。
-
-至于dp,这道题差点我又dp了,但是一看数据范围开不了二维dp,那也dp不了了。
-
-```cpp
-class Solution {
-public:
- int maxArea(vector& height) {
- //长度太大,不能dp
- int len = height.size();
- int left = 0;
- int right = len-1;
- int ans = 0;
- while(left < right){
- ans = max((right-left)*min(height[left],height[right]),ans);
- if(height[left] > height[right]){
- right -= 1;
- }else{
- left += 1;
- }
- }
- return ans;
- }
-};
-```
-
-## 题目链接
-
-[11. 盛最多水的容器 - 力扣(LeetCode)](https://leetcode.cn/problems/container-with-most-water/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode110.md b/algorithms/LeetCode/LeetCode110.md
deleted file mode 100644
index 93c08db..0000000
--- a/algorithms/LeetCode/LeetCode110.md
+++ /dev/null
@@ -1,98 +0,0 @@
----
-title: 平衡二叉树---LeetCode110
-date: 2020-08-17 11:46:25
-tags: [二叉树]
----
-## 题目描述:
-给定一个二叉树,判断它是否是高度平衡的二叉树。
-本题中,一棵高度平衡二叉树定义为:
-一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
-
-## 示例:
-```cpp
-示例 1:
-给定二叉树 [3,9,20,null,null,15,7]
-
- 3
- / \
- 9 20
- / \
- 15 7
-返回 true 。
-
-示例 2:
-给定二叉树 [1,2,2,3,3,null,null,4,4]
-
- 1
- / \
- 2 2
- / \
- 3 3
- / \
- 4 4
-返回 false 。
-```
-
-
-## 解题思路:
-这道题我写了老半天,太菜了呃呃呃.
-说一下思路吧,这道题有两个解法,一个是自顶向下,一个是自底向上。
-### 自顶向下法
-这是一个比较自然的做法,首先要写一个求节点高度的函数(也是用递归实现的),然后对于原树做遍历(先判断自己是不是平衡的,然后再判断左右子树是不平衡的)。但是这个方法有一个不好的地方,就是当你判断一个节点是不是平衡时,你会调用很多次height函数。
-
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-class Solution {
-public:
- int height(TreeNode* root,int depth){
- if(root == NULL) return depth-1;
- return max(height(root->left,depth+1),height(root->right,depth+1));
- }
- bool isBalanced(TreeNode* root) {
- //自顶向下的遍历
- if(root == NULL) return true;
- if(abs(height(root->left,0)-height(root->right,0))>1){
- return false;
- }else{
- return isBalanced(root->left)&&isBalanced(root->right);
- }
- }
-};
-```
-### 自底向上法
-这个方法叫做自底向上法。
-这个方法为什么叫做自底向上法我是这么理解的:当你要求一个节点的高度,你会去求下面的两个节点的高度,然后依次类推,会一直走到叶节点,叶节点的高度为0,然后一路往上推,求出当前节点的高度,而在往上回溯的过程中,如果某个子节点不平衡了,那么就可以一路推上去不平衡(通过return -1)。
-这个方法比起第一个要巧妙了许多,因为你会发现,他对于每一个节点只调用了一次height函数,但是第一种方法会调用多次height函数。
-我想了一下,为什么同样是通过求高度实现,两种方法的差异会如此之大。我认为是这样的:
-1. 第一种方法的本质在于判断当前节点是否平衡,而判断平衡的方法是对于左右节点求高度,然后比较,如此一来,就会求很多次高度,我们可以认为这里有两次递归,一次是在遍历树,一次是在每一次对于一个节点的求高度。
-2. 而第二种方法就仅仅是求高度而已,可以看到,我们实际上就只是求了root高度,而要在求的过程中保存不平衡节点的信息,就通过return -1的方式来实现,真的十分巧妙。
-虽然这是一道简单题,但是真的还是很有意思的。
-```cpp
-class Solution {
-public:
- int height(TreeNode* root){
- if(root == NULL) return 0;
- int leftHeight = height(root->left);
- int rightHeight = height(root->right);
- if(leftHeight == -1 || rightHeight == -1 || abs(leftHeight-rightHeight) > 1){
- return -1;
- }
- return max(leftHeight,rightHeight)+1;
- }
- bool isBalanced(TreeNode* root) {
- if(height(root)>=0) return true;
- return false;
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/balanced-binary-tree/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode121.md b/algorithms/LeetCode/LeetCode121.md
deleted file mode 100644
index c970a3f..0000000
--- a/algorithms/LeetCode/LeetCode121.md
+++ /dev/null
@@ -1,225 +0,0 @@
----
-title: 买卖股票的最佳时机---LeetCode121(dp)
-date: 2023-02-26 20:10:50
-tags: [dp]
----
-# 买卖股票的最佳时机---LeetCode121(dp)
-> 日期: 2023-02-26
-
-## 一次买卖
-
-给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
-
-你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
-
-返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
-### 示例
-
-```
-输入:[7,1,5,3,6,4]
-输出:5
-解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
- 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
-
-来源:力扣(LeetCode)
-链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock
-著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-```
-
-
-
-### 解题思路
-
-用dp做,买卖股票这类题最重要的就是状态的选择,包括后面的差别其实就在状态数量上,以及状态之间是如何转移的。这道题的关键就是只有一次买卖,所以 `dp[i][1]` 如果是当天买的话那么其实就是 `-prices[i]`。
-
-```c++
-class Solution {
-public:
- int maxProfit(vector& prices) {
- int len = prices.size();
- int dp[100005][2]; // dp[i][0] 表示第i天不持有股票时的最大利润, dp[i][i] 表示第i天不持有股票时的最大利润
- memset(dp,0,sizeof(dp));
- dp[0][0] = 0;
- dp[0][1] = -prices[0];
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[30005][2]; //dp[i][0]表示第i天不持有股票的最大利润, //dp[i][1]表示第i天持有股票的最大利润
- memset(dp,0,sizeof(dp));
- dp[0][0] = 0;
- dp[0][1] = -prices[0];
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[100005][5];
- /**
- dp[i][0]表示第i天时还没有进行任何操作
- dp[i][1]表示第i天持有第一个股票的状态
- dp[i][2]表示第i天不持有第一个股票的状态
- dp[i][3]表示第i天持有第二个股票的状态
- dp[i][4]表示第i天不持有第二个股票的状态
- */
- memset(dp,0,sizeof(dp));
- dp[0][1] = -prices[0];
- dp[0][3] = -prices[0]; //这里的初始化很细
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[1010][202]; //每一次交易会增加两种状态
- memset(dp,0,sizeof(dp));
- for(int j=0;j 日期: 2023-08-05
-
-## 题目描述
-二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
-路径和 是路径中各节点值的总和。
-给你一个二叉树的根节点 root ,返回其 最大路径和 。
-
-## 示例
-输入:root = [1,2,3]
-输出:6
-解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
-
-## 解题思路
-xhs面试碰到了,一道不算hard的hard吧。。但是我写成从root出发到叶子的最大路径和了QAQ,反应过来时已经来不及了,哭。
-尤其是事后发现这道题我做过,而且是LeetCode hot100,太悲伤了,引以为戒。
-
-虽然这道题算不上hard,但是还是有一些需要注意的,比如说全局答案的更新和dfs的返回值其实是不同的,原因是这里的dfs的返回值表示的是从一个节点往下走,不走回头路的最大值,所以其实只能选择走左边或者走右边。但是在更新ans的时候就要同时加上左边和右边啦。
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
-class Solution {
-public:
- int ans = INT_MIN;
- int dfs(TreeNode* root){
- if(root == nullptr) return 0;
- int leftMax = max(dfs(root->left), 0);
- int rightMax = max(dfs(root->right), 0);
- ans = max(ans, leftMax + rightMax + root->val);
- return root->val + max(leftMax, rightMax);
- }
- int maxPathSum(TreeNode* root) {
- dfs(root);
- return ans;
- }
-};
-```
-
-
-
-## 题目链接
-https://leetcode.cn/problems/binary-tree-maximum-path-sum/
diff --git a/algorithms/LeetCode/LeetCode134.md b/algorithms/LeetCode/LeetCode134.md
deleted file mode 100644
index 50cae0b..0000000
--- a/algorithms/LeetCode/LeetCode134.md
+++ /dev/null
@@ -1,139 +0,0 @@
----
-title: 加油站---LeetCode134(more than 模拟)
-date: 2020-11-18 13:25:43
-tags: [模拟,智力题]
----
-## 题目描述:
-在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
-
-你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
-
-如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
-
-说明:
-
-如果题目有解,该答案即为唯一答案。
-输入数组均为非空数组,且长度相同。
-输入数组中的元素均为非负数。
-
-
-## 示例:
-```cpp
-这里放测试样例示例 1:
-
-输入:
-gas = [1,2,3,4,5]
-cost = [3,4,5,1,2]
-
-输出: 3
-
-解释:
-从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
-开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
-开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
-开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
-开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
-开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
-因此,3 可为起始索引。
-示例 2:
-
-输入:
-gas = [2,3,4]
-cost = [3,4,3]
-
-输出: -1
-
-解释:
-你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
-我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
-开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
-开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
-你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
-因此,无论怎样,你都不可能绕环路行驶一周。
-```
-
-## 解题思路:
-### 模拟
-这道题一看,呃不就是模拟吗,然后秒了,超过8%(
-```cpp
-class Solution {
-public:
- int canCompleteCircuit(vector& gas, vector& cost) {
- //模拟必超时?
- int len = gas.size();
- int curGas = 0;
- for(int start = 0;start < len;start++){
- curGas = gas[start];
- if(curGas >= cost[start]){
- curGas -= cost[start];
- }else{
- continue;
- }
- int curPos = (start+1)%len;
- while(curPos != start){
- curGas += gas[curPos];
- if(curGas >= cost[curPos]){
- curGas -= cost[curPos];
- }
- else{
- break;
- }
- curPos = (curPos +1)%len;
- }
- if(curPos == start) return start;
- }
- return -1;
- }
-};
-```
-
-### 脑筋急转弯
-但其实这道题有更优的解法,当它说这个题有O(n)解法时,我是不信的,我以为是前缀和什么的,后来我一想,起点又不是固定的,怎么搞,每个节点来一遍前缀和?这好吗?这不好。
-下面贴一段话啊,讲的很形象:
-```cpp
-有一个环形路上有n个站点; 每个站点都有一个好人或一个坏人; 好人会给你钱,坏人会收你一定的过路费,如果你带的钱不够付过路费,坏人会跳起来把你砍死; 问:从哪个站点出发,能绕一圈活着回到出发点?
-
-首先考虑一种情况:如果全部好人给你 的钱加起来 小于 坏人收的过路费之和,那么总有一次你的钱不够付过路费,你的结局注定会被砍死。
-
-假如你随机选一点 start 出发,那么你肯定会选一个有好人的站点开始,因为开始的时候你没有钱,遇到坏人只能被砍死;
-
-现在你在start出发,走到了某个站点end,被end站点的坏人砍死了,说明你在 [start, end) 存的钱不够付 end点坏人的过路费,因为start站点是个好人,所以在 (start, end) 里任何一点出发,你存的钱会比现在还少,还是会被end站点的坏人砍死;
-
-于是你重新读档,聪明的选择从 end+1点出发,继续你悲壮的征程; 终于有一天,你发现自己走到了尽头(下标是n-1)的站点而没有被砍死; 此时你犹豫了一下,那我继续往前走,身上的钱够不够你继续走到出发点Start?
-
-当然可以,因为开始已经判断过,好人给你的钱数是大于等于坏人要的过路费的,你现在攒的钱完全可以应付 [0, start) 这一段坏人向你收的过路费。 这时候你的嘴角微微上扬,眼眶微微湿润,因为你已经知道这个世界的终极奥秘:Start就是这个问题的答案。
-```
-这里面我觉得有两个点很重要。
-一是如果你在start开始,到end死了,那么start到end间的任何一点都不能作为start点,这很好理解。
-还有一个就是走到n-1了,为啥自己就能走回start?这个我还是想了一会的,要保证这个,你首先要满足是从0开始走的。比如我从0开始走,走到4我死了,然后我从5开始走,走到了n-1。这个时候我明显可以走回5,因为如果我在(0,5)死了,那么最后我还是会从5开始走,那就无解了。但是这个明显是有解的,因为**好人给你的钱数是大于等于坏人要的过路费的**。
-这真的不好想到啊,除非是有bear来。
-
-```cpp
-class Solution {
-public:
- int canCompleteCircuit(vector& gas, vector& cost) {
- vector m; // gas和cost相减得到的数组
- int len = gas.size();
- int sum = 0;
- for(int i=0;i
-## 解题思路:
-### 状压dp
-这道题一看就是状态压缩,于是我首先就写了一发状压dp,但是因为s太长了,这里开的dp是二维的,最后就爆内存了。
-其实这种状态压缩的写法并不好,写的时候就感觉很奇怪,之所以奇怪是因为这道题本质上是前缀和,可以用一维的来写,我偏偏写成了二维,最后写出来反正也爆内存了,不过至少这种方法是对的。
-```cpp
-const int MAXN= 10000;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //状压dp?
- int dp[MAXN][MAXN]; //居然可以开这么大 dp[i][j]代表的是从index i到j五个元音的出现情况
- memset(dp,0,sizeof(dp));
- int ans = 0;
- //初始化dp
- int length = s.length();
- for(int i=0;i
-
-### 前缀和
-发现这道题实际上是前缀和后,我立马写了一发前缀和,然后又超时了。
-```cpp
-const int MAXN= 500050;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //前缀和
- int prefix[MAXN];
- memset(prefix,0,sizeof(prefix));
- int ans =0;
- if(s[0] == 'a' ) prefix[0] ^= 1;
- if(s[0] == 'e' ) prefix[0] ^= 2;
- if(s[0] == 'i' ) prefix[0] ^= 4;
- if(s[0] == 'o' ) prefix[0] ^= 8;
- if(s[0] == 'u' ) prefix[0] ^= 16;
-
- int len = s.length();
- for(int i=1;i
-
-### 前缀和+哈希优化
-当我发现前缀和超时了,我就猜到这道题多半要用到哈希优化了(难道是前缀和基本操作吗)。
-当前缀和加上哈希优化,最显著的变化就是不需要再开前缀和数组了,直接拿一个值一直累加(累亦或)下去就行了,以前还碰到一道[前缀和+哈希的题](https://www.assskiller.cn/2020/05/15/LeetCode560/),可以看一下。
-可以把式子稍微推一下,目标是找到prefrx[i] ^ prefix[j-1] = 0,变换一下可以变成prefix[i] = prefix[j-1]。这样一变就很明显了,把前缀和一直类推下去,然后把出现过的值的最小坐标记录一下,再次碰到时,将两个Index减一下就行了。
-需要注意的是需要把records[0]设置为-1,同时还要标记当前的值是否出现过,那就只好把没出现过的值设置为-2了。(我感觉这种做法比较weird,但是至少是对的)。
-```cpp
-const int MAXN= 500050;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //前缀和 + 哈希优化
- int records[100]; //用来记录已经出现的值的位置 records[x]=i;表示前缀和为x的index为i
- for(int i=0;i<100;i++) records[i] = -2; //-2表示没有访问过
- int length =s.length();
- int cur=0;
- int ans=0;
- records[0] = -1;
- for(int i=0;i 日期: 2023-02-20
-
-## 题目描述
-
-给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
-
-注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
-
-## 示例
-
-```
-输入: s = "leetcode", wordDict = ["leet", "code"]
-输出: true
-解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
-
-```
-
-```
-输入: s = "applepenapple", wordDict = ["apple", "pen"]
-输出: true
-解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
- 注意,你可以重复使用字典中的单词。
-```
-
-```
-输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
-输出: false
-```
-
-
-
-## 解题思路
-
-### 备忘录思路
-
-个人感觉使用dfs + 备忘录的方式会更加清晰,所以把这个题解放在前面。
-
-```cpp
-class Solution {
-public:
- // dfs + 备忘录写法
- map, bool> m;
- bool dfs(string& s, int idx, vector& wordDict){
- if(idx == s.size()) return true;
- if(m.count(make_pair(s,idx))) return m[make_pair(s,idx)];
- bool ans = false;
- for(string& word:wordDict){
- if(s.size() - idx < word.size()) continue;
- bool valid = true;
- for(int i=0;i& wordDict) {
- return dfs(s, 0, wordDict);
- }
-};
-```
-
-
-
-### 背包思路
-
-首先,可以重复使用,所以判断为完全背包。
-
-因为顺序是很重要的,比如说 leetcode 是 由 leet 和 code 组成的,而不是由 code 和 leet 组成的,所以完全背包应该先遍历容量,再遍历物品。
-
-然后就可以dp了
-
-```cpp
-class Solution {
-public:
- bool wordBreak(string s, vector& wordDict) {
- unordered_set wordSet(wordDict.begin(), wordDict.end());
- //完全背包
- vector dp(s.size() + 1, false);
- dp[0] = true;
- for(int i=1;i<=s.size();i++){
- for(int j=0; j 其实像这种和传统的背包问题已经不是特别像的题,感觉也不是特别有必要把思路往背包上面靠了,直接想dp说不定还更容易一些(可能吧)
-
-
-
-## 题目链接
-
-[139. 单词拆分 - 力扣(LeetCode)](https://leetcode.cn/problems/word-break/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode144.md b/algorithms/LeetCode/LeetCode144.md
deleted file mode 100644
index b62da26..0000000
--- a/algorithms/LeetCode/LeetCode144.md
+++ /dev/null
@@ -1,68 +0,0 @@
----
-title: 二叉树的前序遍历---LeetCode144
-date: 2020-10-27 11:24:49
-tags: [栈,Stack]
----
-## 题目描述:
-给定一个二叉树,返回它的 前序 遍历。
-
-## 示例:
-```cpp
-示例:
-输入: [1,null,2,3]
- 1
- \
- 2
- /
- 3
-
-输出: [1,2,3]
-```
-
-
-## 解题思路:
-好久没写博客了,或者说好久没写leetcode了= =,来水一发。
-水题,两种方法,一个递归,一个迭代。
-### 递归
-```cpp
-class Solution {
-public:
- vector ans;
- void dfs(TreeNode* root){
- if(root == nullptr) return;
- ans.push_back(root->val);
- dfs(root->left);
- dfs(root->right);
- }
- vector preorderTraversal(TreeNode* root) {
- ans.clear();
- dfs(root);
- return ans;
- }
-};
-```
-
-### 迭代
-迭代时使用的是栈,要注意,栈是先push右边,再push左边,因为需要在pop时先pop左边,再pop右边。
-```cpp
-class Solution {
-public:
- vector preorderTraversal(TreeNode* root) {
- vector ans;
- //stack
- stack s;
- if(root!=nullptr) s.push(root);
- while(!s.empty()){
- TreeNode* topNode = s.top();
- s.pop();
- ans.push_back(topNode->val);
- if(topNode->right != nullptr) s.push(topNode->right);
- if(topNode->left != nullptr) s.push(topNode->left);
- }
- return ans;
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1458.md b/algorithms/LeetCode/LeetCode1458.md
deleted file mode 100644
index b1cf503..0000000
--- a/algorithms/LeetCode/LeetCode1458.md
+++ /dev/null
@@ -1,76 +0,0 @@
----
-title: 两个子序列的最大点积---LeetCode1458(双序列dp)
-date: 2020-05-26 00:16:05
-tags: [双序列dp]
----
-## 题目描述:
-给你两个数组 nums1 和 nums2 。
-请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。
-数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。
-
-
-## 示例:
-```cpp
-示例 1:
-输入:nums1 = [2,1,-2,5], nums2 = [3,0,-6]
-输出:18
-解释:从 nums1 中得到子序列 [2,-2] ,从 nums2 中得到子序列 [3,-6] 。
-它们的点积为 (2*3 + (-2)*(-6)) = 18 。
-
-示例 2:
-输入:nums1 = [3,-2], nums2 = [2,-6,7]
-输出:21
-解释:从 nums1 中得到子序列 [3] ,从 nums2 中得到子序列 [7] 。
-它们的点积为 (3*7) = 21 。
-
-示例 3:
-输入:nums1 = [-1,-1], nums2 = [1,1]
-输出:-1
-解释:从 nums1 中得到子序列 [-1] ,从 nums2 中得到子序列 [1] 。
-它们的点积为 -1 。
-
-提示:
-1 <= nums1.length, nums2.length <= 500
--1000 <= nums1[i], nums2[i] <= 100
-
-```
-
-## 解题思路:
-记录一下双序列dp,当时直接写没写出来,看了解答后发现也不是很难。
-这个题和最大公共子序列,和那个编辑距离(还没做过)貌似很像,像这种双序列的dp一般是有套路的,都是像下面那种,**dp[i][j] = max(dp[i-1][j-1]+xxx, dp[i][j-1], dp[i-1][j])** 这种的吧。
-算是在leetcode上第一次碰到这种类型吧,记录一下。
-
-```cpp
-const int MAXN = 550;
-class Solution {
-public:
- int maxDotProduct(vector& nums1, vector& nums2) {
- //双序列dp
- int dp[MAXN][MAXN]; //dp[i][j]表示Nums1的从0到indexi个元素和nums2的从0到Indexj个元素的最小点积
- int length1 = nums1.size();
- int length2 = nums2.size();
- //初始化
- for(int i=0;i0 && j>0)dp[i][j] = max(dp[i][j],dp[i-1][j-1] + nums1[i]*nums2[j]);
- if(i>0) dp[i][j] = max(dp[i][j],dp[i-1][j]);
- if(j>0) dp[i][j] = max(dp[i][j],dp[i][j-1]);
- }
- }
- return dp[length1-1][length2-1];
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/max-dot-product-of-two-subsequences/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode146.md b/algorithms/LeetCode/LeetCode146.md
deleted file mode 100644
index 3dc3b46..0000000
--- a/algorithms/LeetCode/LeetCode146.md
+++ /dev/null
@@ -1,245 +0,0 @@
----
-title: LRU缓存机制---LeetCode146(链表好像变香了)
-date: 2020-05-25 21:43:13
-tags: [哈希, 链表]
----
-## 题目描述:
-运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
-获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
-写入数据 put(key, value) - 如果密钥已经存在,则变更其数据值;如果密钥不存在,则插入该组「密钥/数据值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
-进阶:
-你是否可以在 O(1) 时间复杂度内完成这两种操作?
-
-## 示例:
-```cpp
-LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
-cache.put(1, 1);
-cache.put(2, 2);
-cache.get(1); // 返回 1
-cache.put(3, 3); // 该操作会使得密钥 2 作废
-cache.get(2); // 返回 -1 (未找到)
-cache.put(4, 4); // 该操作会使得密钥 1 作废
-cache.get(1); // 返回 -1 (未找到)
-cache.get(3); // 返回 3
-cache.get(4); // 返回 4
-```
-
-## 解题思路:
-这道题注意要各种分类讨论的细节,即先分为Key是否在当前缓存中,如果在,就直接改,如果不在,还要看当前是否已经到达了最大capacity,没到就直接加,到了就要加+删。
-这道题我还是说两个解法吧,虽然第一个不是O1,但也是我第一个想到的方法,第二方法就是O1了。
-### 不是O(1)的做法
-用两个map,一个就是直接存键值对,另一个存键-时间对,然后每次去遍历看哪个键的时间最小。
-```cpp
-class LRUCache {
-public:
- map record; //使用一个map来记录键值
- map key_time; //记录键进入的时间
- int time;
- int curNum;
- int size;
-
-
- LRUCache(int capacity) {
- time = 0;
- curNum = 0;
- size = capacity;
- }
-
- int get(int key) {
- time++;
- if(record[key] != 0)
- {
- key_time[key] = time;
- return record[key];
- }
-
- return -1;
- }
-
- void put(int key, int value) {
- time++;
- //如果key存在,直接更新
- if(record[key] != 0)
- {
- record[key] = value;
- key_time[key] = time;
- }
-
- else
- {
- //如果不存在,先找出最小的
- map::iterator iter = key_time.begin();
- int minKey = 0;
- int minTime = 999999;
- while(iter != key_time.end()) {
- if(iter->second < minTime)
- {
- minTime = iter->second;
- minKey = iter->first;
- }
- iter++;
- }
-
- //cout<<"当前Minkey"<get(key);
- * obj->put(key,value);
- */
-```
-
-
-
-### O(1)做法
-O(1)做法使用的是哈希表+双向链表,这次的双向链表比起以前写链表感觉要简单了许多,主要是要先把虚拟节点创好,这样就十分方便。
-在这个方法中,哈希表存得是key-节点指针,双向链表可以用来表示一个key的优先度,最近被使用的在表头,最久不被使用的在表尾巴,双向链表将一个节点移动到表头,添加节点到表头,从表尾删除节点都是O(1),就非常适合这道题。
-```cpp
-struct Node{
- int key;
- int val;
- Node* prev;
- Node* next;
- Node(int k,int v): key(k),val(v), prev(NULL), next(NULL) {}
-};
-class LRUCache {
-public:
- Node* head;
- Node* tail;
- int size;
- int curSize;
- map record; //哈希表里存key与对应在链表里的地址
-
- LRUCache(int capacity) {
- size = capacity;
- curSize = 0;
- head = new Node(0,0);
- tail = new Node(0,0);
- head->next = tail;
- tail->prev = head;
- }
-
- int get(int key) {
- if(record[key] != NULL)
- {
- moveToFront(record[key]);//把它放到前面去
- //printList();
- return record[key]->val;
- }
- else
- {
- //printList();
- return -1;
- }
- }
-
- void put(int key, int value) {
- //如果key存在,直接修改值,并把它移动到表头
- if(record[key] != NULL)
- {
- moveToFront(record[key]);
- record[key]->val = value;
- }
- //如果key不存在
- else
- {
- //如果长度小于capacity,直接添加到表头
- if(curSize < size)
- {
- Node* newNode = new Node(key,value);
- addToFront(newNode);
- record[key] = newNode;
- curSize++;
- }
- //添加到表头,删除表尾元素
- else
- {
- Node* newNode = new Node(key,value);
- addToFront(newNode);
- record[key] = newNode;
- deleteFromEnd();
- }
- }
- //printList();
- }
-
- void addToFront(Node* node)
- {
- node->next = head->next;
- node->prev = head;
- head->next->prev = node;
- head->next = node;
- }
-
- void moveToFront(Node* node)
- {
- node->prev->next = node->next;
- node->next->prev = node->prev;
- addToFront(node);
- }
-
- void deleteFromEnd()
- {
- if(tail->prev == head) return;
-
- record[tail->prev->key] = NULL;
- tail->prev->prev->next = tail;
- tail->prev = tail->prev->prev;
- }
-
- void printList()
- {
- Node* ptr = head;
- while(ptr != NULL)
- {
- cout<val<<"->";
- ptr=ptr->next;
- }
- cout<get(key);
- * obj->put(key,value);
- */
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/lru-cache/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode148.md b/algorithms/LeetCode/LeetCode148.md
deleted file mode 100644
index bd00fa1..0000000
--- a/algorithms/LeetCode/LeetCode148.md
+++ /dev/null
@@ -1,118 +0,0 @@
----
-title: 排序链表---LeetCode148
-date: 2023-09-17 21:25:25
-tags: [mergeSort, 归并, 链表]
----
-# 排序链表---LeetCode148
-> 日期: 2023-09-17
-
-## 题目描述
-
-给你链表的头结点 `head` ,请将其按 **升序** 排列并返回 **排序后的链表** 。
-
-## 示例
-
-```
-输入:head = [4,2,1,3]
-输出:[1,2,3,4]
-```
-
-## 解题思路
-
-这道题要求O(1)空间复杂度,所以还不能用递归的方式来写递归(其实也不好写),要用迭代的方式来写,其中的细节太多啦,所以这里记录一下。
-
-> 顺便一提用递归的方式来写的思路,重点是要对链表一分为二,那么其实就是用快慢指针的方式来找到中点(坑蛮多),然后一分为二。排好序后再merge。这里埋个坑,以后可能会写。
-
-这里记录几个重点:
-
-1. 首先是枚举每一个小段的长度,当然是从1开始,然后每次乘2。
-2. 需要计算一个合并次数,然后按照合并次数写一个loop来执行每一次的合并。在计算合并次数时要注意,如果没除尽的话,那么其实也是需要算是一次合并的(比如对于3个节点,按照段长为1,其实也是要两次合并(1,2 和3,null))。这里可以通过模的方式来判断,也可以直接向上取整。
-3. 每一次合并时,要计算两个链表分别的开头。同时要记录下一次合并的开头,并在最后更新到head。
-4. 在所有的合并计算完后,要记得把cur->next设置为空,来避免链表成环。同时要记得把head还原换取,因为每一次我们是通过更新head来实现更新下一个链表的开头的。
-
-真的很难呢。。。
-
-直接贴代码
-
-```cpp
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode() : val(0), next(nullptr) {}
- * ListNode(int x) : val(x), next(nullptr) {}
- * ListNode(int x, ListNode *next) : val(x), next(next) {}
- * };
- */
-class Solution {
-public:
- ListNode* sortList(ListNode* head) {
- int len = 0;
- ListNode* cur = head;
- while(cur != nullptr){
- len += 1;
- cur = cur->next;
- }
- for(int i=1; i<=len; i*=2){ //枚举长度
- //枚举合并次数
- int cnt = 0;
- if( (len%(i*2)) != 0){
- cnt = len/(i*2) + 1;
- }else{
- cnt = len/(i*2);
- }
- // int cnt = ceil(1.0 * len / (2*i)); //这么写也行
- ListNode* dummy = new ListNode(-1);
- cur = dummy;
- while(cnt--){
- ListNode* l1 = head;
- ListNode* l2 = head;
- //计算l2的开始位置
- for(int j=0;jnext;
- ListNode* nxt = l2;
- //计算下一次开始的位置
- for(int j=0;jnext;
- //每一次合并l1和l2
- int l1Cnt = 0;
- int l2Cnt = 0;
- while(l1Cnt < i && l2Cnt < i && l1 && l2){
- if(l1->val < l2->val){
- l1Cnt += 1;
- cur->next = l1;
- l1 = l1->next;
- }else{
- l2Cnt += 1;
- cur->next = l2;
- l2 = l2->next;
- }
- cur = cur->next;
- }
- while(l1Cnt < i && l1){
- l1Cnt += 1;
- cur->next = l1;
- l1 = l1->next;
- cur = cur->next;
- }
- while(l2Cnt < i && l2){
- l2Cnt += 1;
- cur->next = l2;
- l2 = l2->next;
- cur = cur->next;
- }
- //计算下一个head
- head = nxt;
- }
- cur->next = nullptr; //尾部设置为空,防止成环
- head = dummy->next;
- }
- return head;
- }
-};
-```
-
-
-
-## 题目链接
-
-[148. 排序链表 - 力扣(LeetCode)](https://leetcode.cn/problems/sort-list/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode152.md b/algorithms/LeetCode/LeetCode152.md
deleted file mode 100644
index d6e9a55..0000000
--- a/algorithms/LeetCode/LeetCode152.md
+++ /dev/null
@@ -1,121 +0,0 @@
----
-title: 乘积最大子数组---LeetCode152(不会真的有人以为是前缀和吧)
-date: 2020-05-18 13:39:27
-tags: []
----
-### 题目描述:
-给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
-
-### 示例:
-```cpp
-示例 1:
-输入: [2,3,-2,4]
-输出: 6
-解释: 子数组 [2,3] 有最大乘积 6。
-
-示例 2:
-输入: [-2,0,-1]
-输出: 0
-解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
-```
-
-### 解题思路:
-这道题第一眼看以为是前缀和,秒了!
-然后越写越不对劲,后来发现可能是dp,然后写了一个虚假的dp,再最后发现dp也不需要,搞两个变量记录一下步就行了嘛。
-下面展示一下我是如何一步步优化的。
-ps: 这道题的精髓就是,要使用两个变量来记录,一个最大,一个最小,因为是乘法,所以最大可能下一次就变成最小,最小可能下一次就变成最大,所以都要记录一下。
-### 虚假的dp
-因为计算每一个点时都需要用到前面的,自然而然的想到了dp。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- pair dp[100000]; //dp[i]表示到i为止的最大值,最小值
- dp[0] = make_pair(nums[0],nums[0]);
- int length = nums.size();
- int ans=nums[0];
- for(int i=1;i
-
-### 要什么dp
-但是每次都是只需要前一次的数据,那还要什么dp,白费内存,直接搞两个变量记录一下呗。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- int curMax = nums[0];
- int curMin = nums[0];
- int length = nums.size();
- int ans=nums[0];
- int a,b,mulMax,mulMin;
- for(int i=1;i
-
-### 连比较都不用了
-如果是Nums[i]是负数,那么最大就会变成最小,最小就会变成最大。不然最大还是最大,最小还是最小,所以循环体里面是不用比较的。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- int curMax = nums[0];
- int curMin = nums[0];
- int length = nums.size();
- int ans=nums[0];
- for(int i=1;i 日期: 2023-07-22
-
-二分的红蓝染色法主要用来解决寻找旋转数组里面的一些数的问题,旋转数组是一个前后有序但是总体不有序的数组,因此不能直接套二分来做,需要用来一些巧妙的方法(比如这里的红蓝染色法)来解决。
-
-# 寻找峰值
-
-## 题目描述
-
-峰值元素是指其值严格大于左右相邻值的元素。
-
-给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
-
-你可以假设 nums[-1] = nums[n] = -∞ 。
-
-你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
-
-## 示例
-
-```cpp
-输出:2
-解释:3 是峰值元素,你的函数应该返回其索引 2。
-示例 2:
-
-输入:nums = [1,2,1,3,5,6,4]
-输出:1 或 5
-解释:你的函数可以返回索引 1,其峰值元素为 2;
- 或者返回索引 5, 其峰值元素为 6。
-```
-
-## 解题思路
-
-一般来说,红蓝染色法常用的做法是先去定义红色和蓝色的定义。
-
-比如这道题红色的定义是峰值左边的点,蓝色的定义是**峰值以及峰值右边的点**。
-
-一般来说,这样的定义可以保证最右边一定为蓝色,所以可以把二分的区间缩小到[0,n-2]。
-
-这里是通过比较mid和mid+1位置的点来判断颜色,如果mid的值 > mid+1的值,那么右边肯定全部为蓝色,因为mid就有可能是峰值。否则左边全为红色。
-
-```cpp
-class Solution {
-public:
- int findPeakElement(vector& nums) {
- //红蓝染色法,对于可以确定颜色的区间就不再处理,一直去处理需要决定颜色的区间
- // 定义红色为峰值左边的点,蓝色为峰值右边或者峰值右边的点
- // 那么最右边一定为蓝色,不需要处理
- // 在 [0,n-2]二分
- int left = -1;
- int right = nums.size()-1;
- while(left + 1 < right){
- int mid = (left + right) /2 ;
- if(nums[mid] > nums[mid+1]){
- // 右边全为蓝色
- right = mid;
- }else{
- // 左边全为红色
- left = mid;
- }
- }
- return right;
- }
-};
-```
-
-
-
-# 寻找旋转排序数组中的最小值(无重复数字)
-
-## 题目描述
-
-已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
-若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
-若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
-注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
-
-给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
-
-你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
-
-## 示例
-
-```
-示例 1:
-
-输入:nums = [3,4,5,1,2]
-输出:1
-解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
-示例 2:
-
-输入:nums = [4,5,6,7,0,1,2]
-输出:0
-解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
-示例 3:
-
-输入:nums = [11,13,15,17]
-输出:11
-解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
-
-```
-
-
-
-## 解题思路
-
-一样的红蓝染色法解题。
-
-首先可以确定的是最小值就是旋转点。
-
-把红色定义为在旋转点左侧。
-
-把蓝色定义为**旋转点或者在旋转点右侧**。
-
-同样,最右边一定为蓝色,所以无需纳入考虑范围,在[0,n-2]进行二分。
-
-将mid为最右边的值进行比较,如果mid的值比最右边的值大,那么最小值不可能在左边,所以左边全是红色。
-
-否则右边全是蓝色。
-
-```cpp
-class Solution {
-public:
- int findMin(vector& nums) {
- //红色为旋转点左边
- //蓝色为旋转点或者旋转点右边
- // 因为最右边一定为蓝色,所以在[0,n-2]二分
- int left = -1;
- int right = nums.size()-1;
- while(left + 1 < right){
- int mid = (left + right) / 2;
- if(nums[mid] > nums[nums.size()-1]){
- left = mid;
- }else{
- right = mid;
- }
- }
- return nums[right];
- }
-};
-```
-
-
-
-# 旋转数组的最小数字(有重复)
-
-## 题目描述
-
-把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
-
-给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
-
-注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
-
-## 示例
-
-```
-示例 1:
-
-输入:numbers = [3,4,5,1,2]
-输出:1
-示例 2:
-
-输入:numbers = [2,2,2,0,1]
-输出:0
-
-```
-
-
-
-## 解题思路
-
-这道题和上一题唯一的区别在于有重复数字。
-
-那么如果出现了枚举的mid的值和最右边的数字一样,就不知道该如何判断了。
-
-这里我们的做法是如果一样,那么就right--,不去比较了,这样做也是合理的。
-
-因为如果数字这个值就是最小值,那么--后区间内还存在这个值,不影响。
-
-如果这个值不是最小值,那更无所谓了。
-
-```cpp
-class Solution {
-public:
- int minArray(vector& numbers) {
- //二分
- // 蓝色表示是最小数字或者在最小数字右侧
- // 红色表示在最小数字左侧
- // 因为最右边一定是蓝色,所以在[0,n-2]二分
- int left = -1;
- int right = numbers.size()-1;
- while(left + 1 < right){
- int mid = (left + right) / 2;
- if(numbers[mid] > numbers[right]){
- left = mid;
- }else if(numbers[mid] < numbers[right]){
- right = mid;
- }else{
- right -= 1; //去除末尾元素
- }
- }
- return numbers[right];
- }
-};
-
-```
-
-要注意这里是和`numbers[right]`来比较了而不是之前的`numbers[numbers.size()-1]`
-
-## 题目链接
-
-[162. 寻找峰值 - 力扣(LeetCode)](https://leetcode.cn/problems/find-peak-element/)
-
-[153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)](https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/)
-
-[剑指 Offer 11. 旋转数组的最小数字 - 力扣(LeetCode)](https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/)
-
-[二分查找,一个视频讲透!(Python/Java/C++/Go) - 旋转数组的最小数字 - 力扣(LeetCode)](https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/solution/er-fen-cha-zhao-yi-ge-shi-pin-jiang-tou-1kbvh/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1617.md b/algorithms/LeetCode/LeetCode1617.md
deleted file mode 100644
index b4c21a6..0000000
--- a/algorithms/LeetCode/LeetCode1617.md
+++ /dev/null
@@ -1,200 +0,0 @@
----
-title: 统计子树中城市最大距离---LeetCode1617(子集+树形dp)
-date: 2023-10-20 18:06:39
-tags: [回溯, 树形dp]
----
-# 统计子树中城市最大距离---LeetCode1617(子集+树形dp)
-> 日期: 2023-10-20
-
-## 题目描述
-
-给你 `n` 个城市,编号为从 `1` 到 `n` 。同时给你一个大小为 `n-1` 的数组 `edges` ,其中 `edges[i] = [ui, vi]` 表示城市 `ui` 和 `vi` 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说,所有城市形成了一棵 **树** 。
-
-一棵 **子树** 是城市的一个子集,且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在,但在另一棵子树中不存在。
-
-对于 `d` 从 `1` 到 `n-1` ,请你找到城市间 **最大距离** 恰好为 `d` 的所有子树数目。
-
-请你返回一个大小为 `n-1` 的数组,其中第 `d` 个元素(**下标从 1 开始**)是城市间 **最大距离** 恰好等于 `d` 的子树数目。
-
-**请注意**,两个城市间距离定义为它们之间需要经过的边的数目。
-
-## 示例
-
-```
-输入:n = 4, edges = [[1,2],[2,3],[2,4]]
-输出:[3,4,0]
-解释:
-子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
-子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
-不存在城市间最大距离为 3 的子树。
-```
-
-## 解题思路
-
-### 比较low的求树的直径的写法
-
-我胆子大了敢做hard了,但是这道题其实就是一个树的直径和子集的结合。
-
-因为题目说的最大距离其实就是树的直径,把这个翻译出来其实就好做很多了。
-
-但是细节上的东西还是蛮多的,比如,首先构建出来的子树需要是一个连通的,这里的做法是搞了一个inset和一个vis数组,vis数组在树形dp遍历的时候去更新,最后通过判断vis和inset是否相等来看当前这个子集是不是合法的,只有合法才会去更新答案。
-
-因为树的直径有时候不太能写明白,有时候我会选择把子树的结果全部存进一个vector里面然后挑选最大的两个元素来做(比如这里)
-
-```cpp
-class Solution {
-public:
- // 枚举子集求树的直径
- // 需要更优雅的写法
- vector> g;
- vector vis;
- vector inSet;
- vector ans;
- int N;
- int diameter;
- int dfs(int idx, int fa){
- vis[idx] = true;
- vector tmp;
- for(int son:g[idx]){
- if(son == fa || !inSet[son]) continue;
- int curCnt = dfs(son, idx);
- tmp.push_back(curCnt);
- }
- if(tmp.size() == 0){
- return 1;
- }else if(tmp.size() == 1){
- diameter = max(diameter, tmp[0]);
- return tmp[0] + 1;
- }else{
- sort(tmp.begin(),tmp.end());
- diameter = max(diameter, tmp[tmp.size()-1] + tmp[tmp.size()-2]);
- return tmp[tmp.size()-1] + 1;
- }
- }
-
- void dfs2(int idx){
- if(idx == N){
- // 找一个在子图中的点开始dfs
- for(int i=0;i(N, false);
- diameter = 0;
- dfs(i,-1);
- break;
- }
- }
- if(diameter > 0 && vis == inSet){
- ans[diameter-1]++;
- }
- return;
- }
- inSet[idx] = true;
- dfs2(idx+1);
- inSet[idx] = false;
- dfs2(idx+1);
- }
-
- vector countSubgraphsForEachDiameter(int n, vector>& edges) {
- g = vector>(n);
- inSet = vector(n, false);
- vis = vector(n, false);
- N = n;
- for(auto x : edges){
- g[x[0]-1].push_back(x[1]-1);
- g[x[1]-1].push_back(x[0]-1);
- }
- ans = vector(n-1,0);
- diameter = 0;
- dfs2(0);
- return ans;
-
- }
-};
-```
-
-
-
-### 优雅的求树的直径的写法
-
-不过把所有子树的点数push进vector然后排序的方法比较丑陋,所以还有一种比较绕但是优雅的写法。
-
-这里我们假设dfs的返回值是包含当前节点的最大路径长度,这种写法叫做maxLen。
-
-假设dfs的返回值是包含当前节点的最大节点数量,这种写法叫做maxCnt。
-
-大致就是记录的是maxLen而不是maxCnt了,这种比较好写。因为假设在处理前一颗子树的情况时,如果前面是空,因为我们会把maxCnt初始化为1,但是maxCnt如果最小是1就比较奇怪,但是maxLen是0就很合理。
-
-反正在用maxCnt写法写的时候我不太能想清楚,但是用maxLen写法倒是比较好写。
-
-```cpp
-class Solution {
-public:
- // 枚举子集求树的直径
- vector> g;
- vector
-
-
-
-## 解题思路
-
-这道题是贪心,用两个位置来表示区间,并且判断左右两边的大小,并且移动小的那一边。
-
-这个方法很好想,好像可以通过反证法去证明它不是错的。。。
-
-至于dp,这道题差点我又dp了,但是一看数据范围开不了二维dp,那也dp不了了。
-
-```cpp
-class Solution {
-public:
- int maxArea(vector& height) {
- //长度太大,不能dp
- int len = height.size();
- int left = 0;
- int right = len-1;
- int ans = 0;
- while(left < right){
- ans = max((right-left)*min(height[left],height[right]),ans);
- if(height[left] > height[right]){
- right -= 1;
- }else{
- left += 1;
- }
- }
- return ans;
- }
-};
-```
-
-## 题目链接
-
-[11. 盛最多水的容器 - 力扣(LeetCode)](https://leetcode.cn/problems/container-with-most-water/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode110.md b/algorithms/LeetCode/LeetCode110.md
deleted file mode 100644
index 93c08db..0000000
--- a/algorithms/LeetCode/LeetCode110.md
+++ /dev/null
@@ -1,98 +0,0 @@
----
-title: 平衡二叉树---LeetCode110
-date: 2020-08-17 11:46:25
-tags: [二叉树]
----
-## 题目描述:
-给定一个二叉树,判断它是否是高度平衡的二叉树。
-本题中,一棵高度平衡二叉树定义为:
-一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
-
-## 示例:
-```cpp
-示例 1:
-给定二叉树 [3,9,20,null,null,15,7]
-
- 3
- / \
- 9 20
- / \
- 15 7
-返回 true 。
-
-示例 2:
-给定二叉树 [1,2,2,3,3,null,null,4,4]
-
- 1
- / \
- 2 2
- / \
- 3 3
- / \
- 4 4
-返回 false 。
-```
-
-
-## 解题思路:
-这道题我写了老半天,太菜了呃呃呃.
-说一下思路吧,这道题有两个解法,一个是自顶向下,一个是自底向上。
-### 自顶向下法
-这是一个比较自然的做法,首先要写一个求节点高度的函数(也是用递归实现的),然后对于原树做遍历(先判断自己是不是平衡的,然后再判断左右子树是不平衡的)。但是这个方法有一个不好的地方,就是当你判断一个节点是不是平衡时,你会调用很多次height函数。
-
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode(int x) : val(x), left(NULL), right(NULL) {}
- * };
- */
-class Solution {
-public:
- int height(TreeNode* root,int depth){
- if(root == NULL) return depth-1;
- return max(height(root->left,depth+1),height(root->right,depth+1));
- }
- bool isBalanced(TreeNode* root) {
- //自顶向下的遍历
- if(root == NULL) return true;
- if(abs(height(root->left,0)-height(root->right,0))>1){
- return false;
- }else{
- return isBalanced(root->left)&&isBalanced(root->right);
- }
- }
-};
-```
-### 自底向上法
-这个方法叫做自底向上法。
-这个方法为什么叫做自底向上法我是这么理解的:当你要求一个节点的高度,你会去求下面的两个节点的高度,然后依次类推,会一直走到叶节点,叶节点的高度为0,然后一路往上推,求出当前节点的高度,而在往上回溯的过程中,如果某个子节点不平衡了,那么就可以一路推上去不平衡(通过return -1)。
-这个方法比起第一个要巧妙了许多,因为你会发现,他对于每一个节点只调用了一次height函数,但是第一种方法会调用多次height函数。
-我想了一下,为什么同样是通过求高度实现,两种方法的差异会如此之大。我认为是这样的:
-1. 第一种方法的本质在于判断当前节点是否平衡,而判断平衡的方法是对于左右节点求高度,然后比较,如此一来,就会求很多次高度,我们可以认为这里有两次递归,一次是在遍历树,一次是在每一次对于一个节点的求高度。
-2. 而第二种方法就仅仅是求高度而已,可以看到,我们实际上就只是求了root高度,而要在求的过程中保存不平衡节点的信息,就通过return -1的方式来实现,真的十分巧妙。
-虽然这是一道简单题,但是真的还是很有意思的。
-```cpp
-class Solution {
-public:
- int height(TreeNode* root){
- if(root == NULL) return 0;
- int leftHeight = height(root->left);
- int rightHeight = height(root->right);
- if(leftHeight == -1 || rightHeight == -1 || abs(leftHeight-rightHeight) > 1){
- return -1;
- }
- return max(leftHeight,rightHeight)+1;
- }
- bool isBalanced(TreeNode* root) {
- if(height(root)>=0) return true;
- return false;
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/balanced-binary-tree/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode121.md b/algorithms/LeetCode/LeetCode121.md
deleted file mode 100644
index c970a3f..0000000
--- a/algorithms/LeetCode/LeetCode121.md
+++ /dev/null
@@ -1,225 +0,0 @@
----
-title: 买卖股票的最佳时机---LeetCode121(dp)
-date: 2023-02-26 20:10:50
-tags: [dp]
----
-# 买卖股票的最佳时机---LeetCode121(dp)
-> 日期: 2023-02-26
-
-## 一次买卖
-
-给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
-
-你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
-
-返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
-
-### 示例
-
-```
-输入:[7,1,5,3,6,4]
-输出:5
-解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
- 注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
-
-来源:力扣(LeetCode)
-链接:https://leetcode.cn/problems/best-time-to-buy-and-sell-stock
-著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
-```
-
-
-
-### 解题思路
-
-用dp做,买卖股票这类题最重要的就是状态的选择,包括后面的差别其实就在状态数量上,以及状态之间是如何转移的。这道题的关键就是只有一次买卖,所以 `dp[i][1]` 如果是当天买的话那么其实就是 `-prices[i]`。
-
-```c++
-class Solution {
-public:
- int maxProfit(vector& prices) {
- int len = prices.size();
- int dp[100005][2]; // dp[i][0] 表示第i天不持有股票时的最大利润, dp[i][i] 表示第i天不持有股票时的最大利润
- memset(dp,0,sizeof(dp));
- dp[0][0] = 0;
- dp[0][1] = -prices[0];
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[30005][2]; //dp[i][0]表示第i天不持有股票的最大利润, //dp[i][1]表示第i天持有股票的最大利润
- memset(dp,0,sizeof(dp));
- dp[0][0] = 0;
- dp[0][1] = -prices[0];
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[100005][5];
- /**
- dp[i][0]表示第i天时还没有进行任何操作
- dp[i][1]表示第i天持有第一个股票的状态
- dp[i][2]表示第i天不持有第一个股票的状态
- dp[i][3]表示第i天持有第二个股票的状态
- dp[i][4]表示第i天不持有第二个股票的状态
- */
- memset(dp,0,sizeof(dp));
- dp[0][1] = -prices[0];
- dp[0][3] = -prices[0]; //这里的初始化很细
- for(int i=1;i& prices) {
- int len = prices.size();
- int dp[1010][202]; //每一次交易会增加两种状态
- memset(dp,0,sizeof(dp));
- for(int j=0;j 日期: 2023-08-05
-
-## 题目描述
-二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
-路径和 是路径中各节点值的总和。
-给你一个二叉树的根节点 root ,返回其 最大路径和 。
-
-## 示例
-输入:root = [1,2,3]
-输出:6
-解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
-
-## 解题思路
-xhs面试碰到了,一道不算hard的hard吧。。但是我写成从root出发到叶子的最大路径和了QAQ,反应过来时已经来不及了,哭。
-尤其是事后发现这道题我做过,而且是LeetCode hot100,太悲伤了,引以为戒。
-
-虽然这道题算不上hard,但是还是有一些需要注意的,比如说全局答案的更新和dfs的返回值其实是不同的,原因是这里的dfs的返回值表示的是从一个节点往下走,不走回头路的最大值,所以其实只能选择走左边或者走右边。但是在更新ans的时候就要同时加上左边和右边啦。
-```cpp
-/**
- * Definition for a binary tree node.
- * struct TreeNode {
- * int val;
- * TreeNode *left;
- * TreeNode *right;
- * TreeNode() : val(0), left(nullptr), right(nullptr) {}
- * TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
- * TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
- * };
- */
-class Solution {
-public:
- int ans = INT_MIN;
- int dfs(TreeNode* root){
- if(root == nullptr) return 0;
- int leftMax = max(dfs(root->left), 0);
- int rightMax = max(dfs(root->right), 0);
- ans = max(ans, leftMax + rightMax + root->val);
- return root->val + max(leftMax, rightMax);
- }
- int maxPathSum(TreeNode* root) {
- dfs(root);
- return ans;
- }
-};
-```
-
-
-
-## 题目链接
-https://leetcode.cn/problems/binary-tree-maximum-path-sum/
diff --git a/algorithms/LeetCode/LeetCode134.md b/algorithms/LeetCode/LeetCode134.md
deleted file mode 100644
index 50cae0b..0000000
--- a/algorithms/LeetCode/LeetCode134.md
+++ /dev/null
@@ -1,139 +0,0 @@
----
-title: 加油站---LeetCode134(more than 模拟)
-date: 2020-11-18 13:25:43
-tags: [模拟,智力题]
----
-## 题目描述:
-在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
-
-你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
-
-如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
-
-说明:
-
-如果题目有解,该答案即为唯一答案。
-输入数组均为非空数组,且长度相同。
-输入数组中的元素均为非负数。
-
-
-## 示例:
-```cpp
-这里放测试样例示例 1:
-
-输入:
-gas = [1,2,3,4,5]
-cost = [3,4,5,1,2]
-
-输出: 3
-
-解释:
-从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
-开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
-开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
-开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
-开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
-开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
-因此,3 可为起始索引。
-示例 2:
-
-输入:
-gas = [2,3,4]
-cost = [3,4,3]
-
-输出: -1
-
-解释:
-你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。
-我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油
-开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油
-开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油
-你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。
-因此,无论怎样,你都不可能绕环路行驶一周。
-```
-
-## 解题思路:
-### 模拟
-这道题一看,呃不就是模拟吗,然后秒了,超过8%(
-```cpp
-class Solution {
-public:
- int canCompleteCircuit(vector& gas, vector& cost) {
- //模拟必超时?
- int len = gas.size();
- int curGas = 0;
- for(int start = 0;start < len;start++){
- curGas = gas[start];
- if(curGas >= cost[start]){
- curGas -= cost[start];
- }else{
- continue;
- }
- int curPos = (start+1)%len;
- while(curPos != start){
- curGas += gas[curPos];
- if(curGas >= cost[curPos]){
- curGas -= cost[curPos];
- }
- else{
- break;
- }
- curPos = (curPos +1)%len;
- }
- if(curPos == start) return start;
- }
- return -1;
- }
-};
-```
-
-### 脑筋急转弯
-但其实这道题有更优的解法,当它说这个题有O(n)解法时,我是不信的,我以为是前缀和什么的,后来我一想,起点又不是固定的,怎么搞,每个节点来一遍前缀和?这好吗?这不好。
-下面贴一段话啊,讲的很形象:
-```cpp
-有一个环形路上有n个站点; 每个站点都有一个好人或一个坏人; 好人会给你钱,坏人会收你一定的过路费,如果你带的钱不够付过路费,坏人会跳起来把你砍死; 问:从哪个站点出发,能绕一圈活着回到出发点?
-
-首先考虑一种情况:如果全部好人给你 的钱加起来 小于 坏人收的过路费之和,那么总有一次你的钱不够付过路费,你的结局注定会被砍死。
-
-假如你随机选一点 start 出发,那么你肯定会选一个有好人的站点开始,因为开始的时候你没有钱,遇到坏人只能被砍死;
-
-现在你在start出发,走到了某个站点end,被end站点的坏人砍死了,说明你在 [start, end) 存的钱不够付 end点坏人的过路费,因为start站点是个好人,所以在 (start, end) 里任何一点出发,你存的钱会比现在还少,还是会被end站点的坏人砍死;
-
-于是你重新读档,聪明的选择从 end+1点出发,继续你悲壮的征程; 终于有一天,你发现自己走到了尽头(下标是n-1)的站点而没有被砍死; 此时你犹豫了一下,那我继续往前走,身上的钱够不够你继续走到出发点Start?
-
-当然可以,因为开始已经判断过,好人给你的钱数是大于等于坏人要的过路费的,你现在攒的钱完全可以应付 [0, start) 这一段坏人向你收的过路费。 这时候你的嘴角微微上扬,眼眶微微湿润,因为你已经知道这个世界的终极奥秘:Start就是这个问题的答案。
-```
-这里面我觉得有两个点很重要。
-一是如果你在start开始,到end死了,那么start到end间的任何一点都不能作为start点,这很好理解。
-还有一个就是走到n-1了,为啥自己就能走回start?这个我还是想了一会的,要保证这个,你首先要满足是从0开始走的。比如我从0开始走,走到4我死了,然后我从5开始走,走到了n-1。这个时候我明显可以走回5,因为如果我在(0,5)死了,那么最后我还是会从5开始走,那就无解了。但是这个明显是有解的,因为**好人给你的钱数是大于等于坏人要的过路费的**。
-这真的不好想到啊,除非是有bear来。
-
-```cpp
-class Solution {
-public:
- int canCompleteCircuit(vector& gas, vector& cost) {
- vector m; // gas和cost相减得到的数组
- int len = gas.size();
- int sum = 0;
- for(int i=0;i
-## 解题思路:
-### 状压dp
-这道题一看就是状态压缩,于是我首先就写了一发状压dp,但是因为s太长了,这里开的dp是二维的,最后就爆内存了。
-其实这种状态压缩的写法并不好,写的时候就感觉很奇怪,之所以奇怪是因为这道题本质上是前缀和,可以用一维的来写,我偏偏写成了二维,最后写出来反正也爆内存了,不过至少这种方法是对的。
-```cpp
-const int MAXN= 10000;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //状压dp?
- int dp[MAXN][MAXN]; //居然可以开这么大 dp[i][j]代表的是从index i到j五个元音的出现情况
- memset(dp,0,sizeof(dp));
- int ans = 0;
- //初始化dp
- int length = s.length();
- for(int i=0;i
-
-### 前缀和
-发现这道题实际上是前缀和后,我立马写了一发前缀和,然后又超时了。
-```cpp
-const int MAXN= 500050;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //前缀和
- int prefix[MAXN];
- memset(prefix,0,sizeof(prefix));
- int ans =0;
- if(s[0] == 'a' ) prefix[0] ^= 1;
- if(s[0] == 'e' ) prefix[0] ^= 2;
- if(s[0] == 'i' ) prefix[0] ^= 4;
- if(s[0] == 'o' ) prefix[0] ^= 8;
- if(s[0] == 'u' ) prefix[0] ^= 16;
-
- int len = s.length();
- for(int i=1;i
-
-### 前缀和+哈希优化
-当我发现前缀和超时了,我就猜到这道题多半要用到哈希优化了(难道是前缀和基本操作吗)。
-当前缀和加上哈希优化,最显著的变化就是不需要再开前缀和数组了,直接拿一个值一直累加(累亦或)下去就行了,以前还碰到一道[前缀和+哈希的题](https://www.assskiller.cn/2020/05/15/LeetCode560/),可以看一下。
-可以把式子稍微推一下,目标是找到prefrx[i] ^ prefix[j-1] = 0,变换一下可以变成prefix[i] = prefix[j-1]。这样一变就很明显了,把前缀和一直类推下去,然后把出现过的值的最小坐标记录一下,再次碰到时,将两个Index减一下就行了。
-需要注意的是需要把records[0]设置为-1,同时还要标记当前的值是否出现过,那就只好把没出现过的值设置为-2了。(我感觉这种做法比较weird,但是至少是对的)。
-```cpp
-const int MAXN= 500050;
-class Solution {
-public:
- int findTheLongestSubstring(string s) {
- //前缀和 + 哈希优化
- int records[100]; //用来记录已经出现的值的位置 records[x]=i;表示前缀和为x的index为i
- for(int i=0;i<100;i++) records[i] = -2; //-2表示没有访问过
- int length =s.length();
- int cur=0;
- int ans=0;
- records[0] = -1;
- for(int i=0;i 日期: 2023-02-20
-
-## 题目描述
-
-给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
-
-注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
-
-## 示例
-
-```
-输入: s = "leetcode", wordDict = ["leet", "code"]
-输出: true
-解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
-
-```
-
-```
-输入: s = "applepenapple", wordDict = ["apple", "pen"]
-输出: true
-解释: 返回 true 因为 "applepenapple" 可以由 "apple" "pen" "apple" 拼接成。
- 注意,你可以重复使用字典中的单词。
-```
-
-```
-输入: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
-输出: false
-```
-
-
-
-## 解题思路
-
-### 备忘录思路
-
-个人感觉使用dfs + 备忘录的方式会更加清晰,所以把这个题解放在前面。
-
-```cpp
-class Solution {
-public:
- // dfs + 备忘录写法
- map, bool> m;
- bool dfs(string& s, int idx, vector& wordDict){
- if(idx == s.size()) return true;
- if(m.count(make_pair(s,idx))) return m[make_pair(s,idx)];
- bool ans = false;
- for(string& word:wordDict){
- if(s.size() - idx < word.size()) continue;
- bool valid = true;
- for(int i=0;i& wordDict) {
- return dfs(s, 0, wordDict);
- }
-};
-```
-
-
-
-### 背包思路
-
-首先,可以重复使用,所以判断为完全背包。
-
-因为顺序是很重要的,比如说 leetcode 是 由 leet 和 code 组成的,而不是由 code 和 leet 组成的,所以完全背包应该先遍历容量,再遍历物品。
-
-然后就可以dp了
-
-```cpp
-class Solution {
-public:
- bool wordBreak(string s, vector& wordDict) {
- unordered_set wordSet(wordDict.begin(), wordDict.end());
- //完全背包
- vector dp(s.size() + 1, false);
- dp[0] = true;
- for(int i=1;i<=s.size();i++){
- for(int j=0; j 其实像这种和传统的背包问题已经不是特别像的题,感觉也不是特别有必要把思路往背包上面靠了,直接想dp说不定还更容易一些(可能吧)
-
-
-
-## 题目链接
-
-[139. 单词拆分 - 力扣(LeetCode)](https://leetcode.cn/problems/word-break/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode144.md b/algorithms/LeetCode/LeetCode144.md
deleted file mode 100644
index b62da26..0000000
--- a/algorithms/LeetCode/LeetCode144.md
+++ /dev/null
@@ -1,68 +0,0 @@
----
-title: 二叉树的前序遍历---LeetCode144
-date: 2020-10-27 11:24:49
-tags: [栈,Stack]
----
-## 题目描述:
-给定一个二叉树,返回它的 前序 遍历。
-
-## 示例:
-```cpp
-示例:
-输入: [1,null,2,3]
- 1
- \
- 2
- /
- 3
-
-输出: [1,2,3]
-```
-
-
-## 解题思路:
-好久没写博客了,或者说好久没写leetcode了= =,来水一发。
-水题,两种方法,一个递归,一个迭代。
-### 递归
-```cpp
-class Solution {
-public:
- vector ans;
- void dfs(TreeNode* root){
- if(root == nullptr) return;
- ans.push_back(root->val);
- dfs(root->left);
- dfs(root->right);
- }
- vector preorderTraversal(TreeNode* root) {
- ans.clear();
- dfs(root);
- return ans;
- }
-};
-```
-
-### 迭代
-迭代时使用的是栈,要注意,栈是先push右边,再push左边,因为需要在pop时先pop左边,再pop右边。
-```cpp
-class Solution {
-public:
- vector preorderTraversal(TreeNode* root) {
- vector ans;
- //stack
- stack s;
- if(root!=nullptr) s.push(root);
- while(!s.empty()){
- TreeNode* topNode = s.top();
- s.pop();
- ans.push_back(topNode->val);
- if(topNode->right != nullptr) s.push(topNode->right);
- if(topNode->left != nullptr) s.push(topNode->left);
- }
- return ans;
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/binary-tree-preorder-traversal/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1458.md b/algorithms/LeetCode/LeetCode1458.md
deleted file mode 100644
index b1cf503..0000000
--- a/algorithms/LeetCode/LeetCode1458.md
+++ /dev/null
@@ -1,76 +0,0 @@
----
-title: 两个子序列的最大点积---LeetCode1458(双序列dp)
-date: 2020-05-26 00:16:05
-tags: [双序列dp]
----
-## 题目描述:
-给你两个数组 nums1 和 nums2 。
-请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。
-数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。
-
-
-## 示例:
-```cpp
-示例 1:
-输入:nums1 = [2,1,-2,5], nums2 = [3,0,-6]
-输出:18
-解释:从 nums1 中得到子序列 [2,-2] ,从 nums2 中得到子序列 [3,-6] 。
-它们的点积为 (2*3 + (-2)*(-6)) = 18 。
-
-示例 2:
-输入:nums1 = [3,-2], nums2 = [2,-6,7]
-输出:21
-解释:从 nums1 中得到子序列 [3] ,从 nums2 中得到子序列 [7] 。
-它们的点积为 (3*7) = 21 。
-
-示例 3:
-输入:nums1 = [-1,-1], nums2 = [1,1]
-输出:-1
-解释:从 nums1 中得到子序列 [-1] ,从 nums2 中得到子序列 [1] 。
-它们的点积为 -1 。
-
-提示:
-1 <= nums1.length, nums2.length <= 500
--1000 <= nums1[i], nums2[i] <= 100
-
-```
-
-## 解题思路:
-记录一下双序列dp,当时直接写没写出来,看了解答后发现也不是很难。
-这个题和最大公共子序列,和那个编辑距离(还没做过)貌似很像,像这种双序列的dp一般是有套路的,都是像下面那种,**dp[i][j] = max(dp[i-1][j-1]+xxx, dp[i][j-1], dp[i-1][j])** 这种的吧。
-算是在leetcode上第一次碰到这种类型吧,记录一下。
-
-```cpp
-const int MAXN = 550;
-class Solution {
-public:
- int maxDotProduct(vector& nums1, vector& nums2) {
- //双序列dp
- int dp[MAXN][MAXN]; //dp[i][j]表示Nums1的从0到indexi个元素和nums2的从0到Indexj个元素的最小点积
- int length1 = nums1.size();
- int length2 = nums2.size();
- //初始化
- for(int i=0;i0 && j>0)dp[i][j] = max(dp[i][j],dp[i-1][j-1] + nums1[i]*nums2[j]);
- if(i>0) dp[i][j] = max(dp[i][j],dp[i-1][j]);
- if(j>0) dp[i][j] = max(dp[i][j],dp[i][j-1]);
- }
- }
- return dp[length1-1][length2-1];
- }
-};
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/max-dot-product-of-two-subsequences/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode146.md b/algorithms/LeetCode/LeetCode146.md
deleted file mode 100644
index 3dc3b46..0000000
--- a/algorithms/LeetCode/LeetCode146.md
+++ /dev/null
@@ -1,245 +0,0 @@
----
-title: LRU缓存机制---LeetCode146(链表好像变香了)
-date: 2020-05-25 21:43:13
-tags: [哈希, 链表]
----
-## 题目描述:
-运用你所掌握的数据结构,设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作: 获取数据 get 和 写入数据 put 。
-获取数据 get(key) - 如果密钥 (key) 存在于缓存中,则获取密钥的值(总是正数),否则返回 -1。
-写入数据 put(key, value) - 如果密钥已经存在,则变更其数据值;如果密钥不存在,则插入该组「密钥/数据值」。当缓存容量达到上限时,它应该在写入新数据之前删除最久未使用的数据值,从而为新的数据值留出空间。
-进阶:
-你是否可以在 O(1) 时间复杂度内完成这两种操作?
-
-## 示例:
-```cpp
-LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );
-cache.put(1, 1);
-cache.put(2, 2);
-cache.get(1); // 返回 1
-cache.put(3, 3); // 该操作会使得密钥 2 作废
-cache.get(2); // 返回 -1 (未找到)
-cache.put(4, 4); // 该操作会使得密钥 1 作废
-cache.get(1); // 返回 -1 (未找到)
-cache.get(3); // 返回 3
-cache.get(4); // 返回 4
-```
-
-## 解题思路:
-这道题注意要各种分类讨论的细节,即先分为Key是否在当前缓存中,如果在,就直接改,如果不在,还要看当前是否已经到达了最大capacity,没到就直接加,到了就要加+删。
-这道题我还是说两个解法吧,虽然第一个不是O1,但也是我第一个想到的方法,第二方法就是O1了。
-### 不是O(1)的做法
-用两个map,一个就是直接存键值对,另一个存键-时间对,然后每次去遍历看哪个键的时间最小。
-```cpp
-class LRUCache {
-public:
- map record; //使用一个map来记录键值
- map key_time; //记录键进入的时间
- int time;
- int curNum;
- int size;
-
-
- LRUCache(int capacity) {
- time = 0;
- curNum = 0;
- size = capacity;
- }
-
- int get(int key) {
- time++;
- if(record[key] != 0)
- {
- key_time[key] = time;
- return record[key];
- }
-
- return -1;
- }
-
- void put(int key, int value) {
- time++;
- //如果key存在,直接更新
- if(record[key] != 0)
- {
- record[key] = value;
- key_time[key] = time;
- }
-
- else
- {
- //如果不存在,先找出最小的
- map::iterator iter = key_time.begin();
- int minKey = 0;
- int minTime = 999999;
- while(iter != key_time.end()) {
- if(iter->second < minTime)
- {
- minTime = iter->second;
- minKey = iter->first;
- }
- iter++;
- }
-
- //cout<<"当前Minkey"<get(key);
- * obj->put(key,value);
- */
-```
-
-
-
-### O(1)做法
-O(1)做法使用的是哈希表+双向链表,这次的双向链表比起以前写链表感觉要简单了许多,主要是要先把虚拟节点创好,这样就十分方便。
-在这个方法中,哈希表存得是key-节点指针,双向链表可以用来表示一个key的优先度,最近被使用的在表头,最久不被使用的在表尾巴,双向链表将一个节点移动到表头,添加节点到表头,从表尾删除节点都是O(1),就非常适合这道题。
-```cpp
-struct Node{
- int key;
- int val;
- Node* prev;
- Node* next;
- Node(int k,int v): key(k),val(v), prev(NULL), next(NULL) {}
-};
-class LRUCache {
-public:
- Node* head;
- Node* tail;
- int size;
- int curSize;
- map record; //哈希表里存key与对应在链表里的地址
-
- LRUCache(int capacity) {
- size = capacity;
- curSize = 0;
- head = new Node(0,0);
- tail = new Node(0,0);
- head->next = tail;
- tail->prev = head;
- }
-
- int get(int key) {
- if(record[key] != NULL)
- {
- moveToFront(record[key]);//把它放到前面去
- //printList();
- return record[key]->val;
- }
- else
- {
- //printList();
- return -1;
- }
- }
-
- void put(int key, int value) {
- //如果key存在,直接修改值,并把它移动到表头
- if(record[key] != NULL)
- {
- moveToFront(record[key]);
- record[key]->val = value;
- }
- //如果key不存在
- else
- {
- //如果长度小于capacity,直接添加到表头
- if(curSize < size)
- {
- Node* newNode = new Node(key,value);
- addToFront(newNode);
- record[key] = newNode;
- curSize++;
- }
- //添加到表头,删除表尾元素
- else
- {
- Node* newNode = new Node(key,value);
- addToFront(newNode);
- record[key] = newNode;
- deleteFromEnd();
- }
- }
- //printList();
- }
-
- void addToFront(Node* node)
- {
- node->next = head->next;
- node->prev = head;
- head->next->prev = node;
- head->next = node;
- }
-
- void moveToFront(Node* node)
- {
- node->prev->next = node->next;
- node->next->prev = node->prev;
- addToFront(node);
- }
-
- void deleteFromEnd()
- {
- if(tail->prev == head) return;
-
- record[tail->prev->key] = NULL;
- tail->prev->prev->next = tail;
- tail->prev = tail->prev->prev;
- }
-
- void printList()
- {
- Node* ptr = head;
- while(ptr != NULL)
- {
- cout<val<<"->";
- ptr=ptr->next;
- }
- cout<get(key);
- * obj->put(key,value);
- */
-```
-
-## 题目链接:
-https://leetcode-cn.com/problems/lru-cache/
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode148.md b/algorithms/LeetCode/LeetCode148.md
deleted file mode 100644
index bd00fa1..0000000
--- a/algorithms/LeetCode/LeetCode148.md
+++ /dev/null
@@ -1,118 +0,0 @@
----
-title: 排序链表---LeetCode148
-date: 2023-09-17 21:25:25
-tags: [mergeSort, 归并, 链表]
----
-# 排序链表---LeetCode148
-> 日期: 2023-09-17
-
-## 题目描述
-
-给你链表的头结点 `head` ,请将其按 **升序** 排列并返回 **排序后的链表** 。
-
-## 示例
-
-```
-输入:head = [4,2,1,3]
-输出:[1,2,3,4]
-```
-
-## 解题思路
-
-这道题要求O(1)空间复杂度,所以还不能用递归的方式来写递归(其实也不好写),要用迭代的方式来写,其中的细节太多啦,所以这里记录一下。
-
-> 顺便一提用递归的方式来写的思路,重点是要对链表一分为二,那么其实就是用快慢指针的方式来找到中点(坑蛮多),然后一分为二。排好序后再merge。这里埋个坑,以后可能会写。
-
-这里记录几个重点:
-
-1. 首先是枚举每一个小段的长度,当然是从1开始,然后每次乘2。
-2. 需要计算一个合并次数,然后按照合并次数写一个loop来执行每一次的合并。在计算合并次数时要注意,如果没除尽的话,那么其实也是需要算是一次合并的(比如对于3个节点,按照段长为1,其实也是要两次合并(1,2 和3,null))。这里可以通过模的方式来判断,也可以直接向上取整。
-3. 每一次合并时,要计算两个链表分别的开头。同时要记录下一次合并的开头,并在最后更新到head。
-4. 在所有的合并计算完后,要记得把cur->next设置为空,来避免链表成环。同时要记得把head还原换取,因为每一次我们是通过更新head来实现更新下一个链表的开头的。
-
-真的很难呢。。。
-
-直接贴代码
-
-```cpp
-/**
- * Definition for singly-linked list.
- * struct ListNode {
- * int val;
- * ListNode *next;
- * ListNode() : val(0), next(nullptr) {}
- * ListNode(int x) : val(x), next(nullptr) {}
- * ListNode(int x, ListNode *next) : val(x), next(next) {}
- * };
- */
-class Solution {
-public:
- ListNode* sortList(ListNode* head) {
- int len = 0;
- ListNode* cur = head;
- while(cur != nullptr){
- len += 1;
- cur = cur->next;
- }
- for(int i=1; i<=len; i*=2){ //枚举长度
- //枚举合并次数
- int cnt = 0;
- if( (len%(i*2)) != 0){
- cnt = len/(i*2) + 1;
- }else{
- cnt = len/(i*2);
- }
- // int cnt = ceil(1.0 * len / (2*i)); //这么写也行
- ListNode* dummy = new ListNode(-1);
- cur = dummy;
- while(cnt--){
- ListNode* l1 = head;
- ListNode* l2 = head;
- //计算l2的开始位置
- for(int j=0;jnext;
- ListNode* nxt = l2;
- //计算下一次开始的位置
- for(int j=0;jnext;
- //每一次合并l1和l2
- int l1Cnt = 0;
- int l2Cnt = 0;
- while(l1Cnt < i && l2Cnt < i && l1 && l2){
- if(l1->val < l2->val){
- l1Cnt += 1;
- cur->next = l1;
- l1 = l1->next;
- }else{
- l2Cnt += 1;
- cur->next = l2;
- l2 = l2->next;
- }
- cur = cur->next;
- }
- while(l1Cnt < i && l1){
- l1Cnt += 1;
- cur->next = l1;
- l1 = l1->next;
- cur = cur->next;
- }
- while(l2Cnt < i && l2){
- l2Cnt += 1;
- cur->next = l2;
- l2 = l2->next;
- cur = cur->next;
- }
- //计算下一个head
- head = nxt;
- }
- cur->next = nullptr; //尾部设置为空,防止成环
- head = dummy->next;
- }
- return head;
- }
-};
-```
-
-
-
-## 题目链接
-
-[148. 排序链表 - 力扣(LeetCode)](https://leetcode.cn/problems/sort-list/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode152.md b/algorithms/LeetCode/LeetCode152.md
deleted file mode 100644
index d6e9a55..0000000
--- a/algorithms/LeetCode/LeetCode152.md
+++ /dev/null
@@ -1,121 +0,0 @@
----
-title: 乘积最大子数组---LeetCode152(不会真的有人以为是前缀和吧)
-date: 2020-05-18 13:39:27
-tags: []
----
-### 题目描述:
-给你一个整数数组 nums ,请你找出数组中乘积最大的连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
-
-### 示例:
-```cpp
-示例 1:
-输入: [2,3,-2,4]
-输出: 6
-解释: 子数组 [2,3] 有最大乘积 6。
-
-示例 2:
-输入: [-2,0,-1]
-输出: 0
-解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
-```
-
-### 解题思路:
-这道题第一眼看以为是前缀和,秒了!
-然后越写越不对劲,后来发现可能是dp,然后写了一个虚假的dp,再最后发现dp也不需要,搞两个变量记录一下步就行了嘛。
-下面展示一下我是如何一步步优化的。
-ps: 这道题的精髓就是,要使用两个变量来记录,一个最大,一个最小,因为是乘法,所以最大可能下一次就变成最小,最小可能下一次就变成最大,所以都要记录一下。
-### 虚假的dp
-因为计算每一个点时都需要用到前面的,自然而然的想到了dp。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- pair dp[100000]; //dp[i]表示到i为止的最大值,最小值
- dp[0] = make_pair(nums[0],nums[0]);
- int length = nums.size();
- int ans=nums[0];
- for(int i=1;i
-
-### 要什么dp
-但是每次都是只需要前一次的数据,那还要什么dp,白费内存,直接搞两个变量记录一下呗。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- int curMax = nums[0];
- int curMin = nums[0];
- int length = nums.size();
- int ans=nums[0];
- int a,b,mulMax,mulMin;
- for(int i=1;i
-
-### 连比较都不用了
-如果是Nums[i]是负数,那么最大就会变成最小,最小就会变成最大。不然最大还是最大,最小还是最小,所以循环体里面是不用比较的。
-```cpp
-class Solution {
-public:
- int maxProduct(vector& nums) {
- int curMax = nums[0];
- int curMin = nums[0];
- int length = nums.size();
- int ans=nums[0];
- for(int i=1;i 日期: 2023-07-22
-
-二分的红蓝染色法主要用来解决寻找旋转数组里面的一些数的问题,旋转数组是一个前后有序但是总体不有序的数组,因此不能直接套二分来做,需要用来一些巧妙的方法(比如这里的红蓝染色法)来解决。
-
-# 寻找峰值
-
-## 题目描述
-
-峰值元素是指其值严格大于左右相邻值的元素。
-
-给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
-
-你可以假设 nums[-1] = nums[n] = -∞ 。
-
-你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
-
-## 示例
-
-```cpp
-输出:2
-解释:3 是峰值元素,你的函数应该返回其索引 2。
-示例 2:
-
-输入:nums = [1,2,1,3,5,6,4]
-输出:1 或 5
-解释:你的函数可以返回索引 1,其峰值元素为 2;
- 或者返回索引 5, 其峰值元素为 6。
-```
-
-## 解题思路
-
-一般来说,红蓝染色法常用的做法是先去定义红色和蓝色的定义。
-
-比如这道题红色的定义是峰值左边的点,蓝色的定义是**峰值以及峰值右边的点**。
-
-一般来说,这样的定义可以保证最右边一定为蓝色,所以可以把二分的区间缩小到[0,n-2]。
-
-这里是通过比较mid和mid+1位置的点来判断颜色,如果mid的值 > mid+1的值,那么右边肯定全部为蓝色,因为mid就有可能是峰值。否则左边全为红色。
-
-```cpp
-class Solution {
-public:
- int findPeakElement(vector& nums) {
- //红蓝染色法,对于可以确定颜色的区间就不再处理,一直去处理需要决定颜色的区间
- // 定义红色为峰值左边的点,蓝色为峰值右边或者峰值右边的点
- // 那么最右边一定为蓝色,不需要处理
- // 在 [0,n-2]二分
- int left = -1;
- int right = nums.size()-1;
- while(left + 1 < right){
- int mid = (left + right) /2 ;
- if(nums[mid] > nums[mid+1]){
- // 右边全为蓝色
- right = mid;
- }else{
- // 左边全为红色
- left = mid;
- }
- }
- return right;
- }
-};
-```
-
-
-
-# 寻找旋转排序数组中的最小值(无重复数字)
-
-## 题目描述
-
-已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
-若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
-若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
-注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
-
-给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
-
-你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
-
-## 示例
-
-```
-示例 1:
-
-输入:nums = [3,4,5,1,2]
-输出:1
-解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
-示例 2:
-
-输入:nums = [4,5,6,7,0,1,2]
-输出:0
-解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
-示例 3:
-
-输入:nums = [11,13,15,17]
-输出:11
-解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
-
-```
-
-
-
-## 解题思路
-
-一样的红蓝染色法解题。
-
-首先可以确定的是最小值就是旋转点。
-
-把红色定义为在旋转点左侧。
-
-把蓝色定义为**旋转点或者在旋转点右侧**。
-
-同样,最右边一定为蓝色,所以无需纳入考虑范围,在[0,n-2]进行二分。
-
-将mid为最右边的值进行比较,如果mid的值比最右边的值大,那么最小值不可能在左边,所以左边全是红色。
-
-否则右边全是蓝色。
-
-```cpp
-class Solution {
-public:
- int findMin(vector& nums) {
- //红色为旋转点左边
- //蓝色为旋转点或者旋转点右边
- // 因为最右边一定为蓝色,所以在[0,n-2]二分
- int left = -1;
- int right = nums.size()-1;
- while(left + 1 < right){
- int mid = (left + right) / 2;
- if(nums[mid] > nums[nums.size()-1]){
- left = mid;
- }else{
- right = mid;
- }
- }
- return nums[right];
- }
-};
-```
-
-
-
-# 旋转数组的最小数字(有重复)
-
-## 题目描述
-
-把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。
-
-给你一个可能存在 重复 元素值的数组 numbers ,它原来是一个升序排列的数组,并按上述情形进行了一次旋转。请返回旋转数组的最小元素。例如,数组 [3,4,5,1,2] 为 [1,2,3,4,5] 的一次旋转,该数组的最小值为 1。
-
-注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
-
-## 示例
-
-```
-示例 1:
-
-输入:numbers = [3,4,5,1,2]
-输出:1
-示例 2:
-
-输入:numbers = [2,2,2,0,1]
-输出:0
-
-```
-
-
-
-## 解题思路
-
-这道题和上一题唯一的区别在于有重复数字。
-
-那么如果出现了枚举的mid的值和最右边的数字一样,就不知道该如何判断了。
-
-这里我们的做法是如果一样,那么就right--,不去比较了,这样做也是合理的。
-
-因为如果数字这个值就是最小值,那么--后区间内还存在这个值,不影响。
-
-如果这个值不是最小值,那更无所谓了。
-
-```cpp
-class Solution {
-public:
- int minArray(vector& numbers) {
- //二分
- // 蓝色表示是最小数字或者在最小数字右侧
- // 红色表示在最小数字左侧
- // 因为最右边一定是蓝色,所以在[0,n-2]二分
- int left = -1;
- int right = numbers.size()-1;
- while(left + 1 < right){
- int mid = (left + right) / 2;
- if(numbers[mid] > numbers[right]){
- left = mid;
- }else if(numbers[mid] < numbers[right]){
- right = mid;
- }else{
- right -= 1; //去除末尾元素
- }
- }
- return numbers[right];
- }
-};
-
-```
-
-要注意这里是和`numbers[right]`来比较了而不是之前的`numbers[numbers.size()-1]`
-
-## 题目链接
-
-[162. 寻找峰值 - 力扣(LeetCode)](https://leetcode.cn/problems/find-peak-element/)
-
-[153. 寻找旋转排序数组中的最小值 - 力扣(LeetCode)](https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/)
-
-[剑指 Offer 11. 旋转数组的最小数字 - 力扣(LeetCode)](https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/)
-
-[二分查找,一个视频讲透!(Python/Java/C++/Go) - 旋转数组的最小数字 - 力扣(LeetCode)](https://leetcode.cn/problems/xuan-zhuan-shu-zu-de-zui-xiao-shu-zi-lcof/solution/er-fen-cha-zhao-yi-ge-shi-pin-jiang-tou-1kbvh/)
\ No newline at end of file
diff --git a/algorithms/LeetCode/LeetCode1617.md b/algorithms/LeetCode/LeetCode1617.md
deleted file mode 100644
index b4c21a6..0000000
--- a/algorithms/LeetCode/LeetCode1617.md
+++ /dev/null
@@ -1,200 +0,0 @@
----
-title: 统计子树中城市最大距离---LeetCode1617(子集+树形dp)
-date: 2023-10-20 18:06:39
-tags: [回溯, 树形dp]
----
-# 统计子树中城市最大距离---LeetCode1617(子集+树形dp)
-> 日期: 2023-10-20
-
-## 题目描述
-
-给你 `n` 个城市,编号为从 `1` 到 `n` 。同时给你一个大小为 `n-1` 的数组 `edges` ,其中 `edges[i] = [ui, vi]` 表示城市 `ui` 和 `vi` 之间有一条双向边。题目保证任意城市之间只有唯一的一条路径。换句话说,所有城市形成了一棵 **树** 。
-
-一棵 **子树** 是城市的一个子集,且子集中任意城市之间可以通过子集中的其他城市和边到达。两个子树被认为不一样的条件是至少有一个城市在其中一棵子树中存在,但在另一棵子树中不存在。
-
-对于 `d` 从 `1` 到 `n-1` ,请你找到城市间 **最大距离** 恰好为 `d` 的所有子树数目。
-
-请你返回一个大小为 `n-1` 的数组,其中第 `d` 个元素(**下标从 1 开始**)是城市间 **最大距离** 恰好等于 `d` 的子树数目。
-
-**请注意**,两个城市间距离定义为它们之间需要经过的边的数目。
-
-## 示例
-
-```
-输入:n = 4, edges = [[1,2],[2,3],[2,4]]
-输出:[3,4,0]
-解释:
-子树 {1,2}, {2,3} 和 {2,4} 最大距离都是 1 。
-子树 {1,2,3}, {1,2,4}, {2,3,4} 和 {1,2,3,4} 最大距离都为 2 。
-不存在城市间最大距离为 3 的子树。
-```
-
-## 解题思路
-
-### 比较low的求树的直径的写法
-
-我胆子大了敢做hard了,但是这道题其实就是一个树的直径和子集的结合。
-
-因为题目说的最大距离其实就是树的直径,把这个翻译出来其实就好做很多了。
-
-但是细节上的东西还是蛮多的,比如,首先构建出来的子树需要是一个连通的,这里的做法是搞了一个inset和一个vis数组,vis数组在树形dp遍历的时候去更新,最后通过判断vis和inset是否相等来看当前这个子集是不是合法的,只有合法才会去更新答案。
-
-因为树的直径有时候不太能写明白,有时候我会选择把子树的结果全部存进一个vector里面然后挑选最大的两个元素来做(比如这里)
-
-```cpp
-class Solution {
-public:
- // 枚举子集求树的直径
- // 需要更优雅的写法
- vector> g;
- vector vis;
- vector inSet;
- vector ans;
- int N;
- int diameter;
- int dfs(int idx, int fa){
- vis[idx] = true;
- vector tmp;
- for(int son:g[idx]){
- if(son == fa || !inSet[son]) continue;
- int curCnt = dfs(son, idx);
- tmp.push_back(curCnt);
- }
- if(tmp.size() == 0){
- return 1;
- }else if(tmp.size() == 1){
- diameter = max(diameter, tmp[0]);
- return tmp[0] + 1;
- }else{
- sort(tmp.begin(),tmp.end());
- diameter = max(diameter, tmp[tmp.size()-1] + tmp[tmp.size()-2]);
- return tmp[tmp.size()-1] + 1;
- }
- }
-
- void dfs2(int idx){
- if(idx == N){
- // 找一个在子图中的点开始dfs
- for(int i=0;i(N, false);
- diameter = 0;
- dfs(i,-1);
- break;
- }
- }
- if(diameter > 0 && vis == inSet){
- ans[diameter-1]++;
- }
- return;
- }
- inSet[idx] = true;
- dfs2(idx+1);
- inSet[idx] = false;
- dfs2(idx+1);
- }
-
- vector countSubgraphsForEachDiameter(int n, vector>& edges) {
- g = vector>(n);
- inSet = vector(n, false);
- vis = vector(n, false);
- N = n;
- for(auto x : edges){
- g[x[0]-1].push_back(x[1]-1);
- g[x[1]-1].push_back(x[0]-1);
- }
- ans = vector(n-1,0);
- diameter = 0;
- dfs2(0);
- return ans;
-
- }
-};
-```
-
-
-
-### 优雅的求树的直径的写法
-
-不过把所有子树的点数push进vector然后排序的方法比较丑陋,所以还有一种比较绕但是优雅的写法。
-
-这里我们假设dfs的返回值是包含当前节点的最大路径长度,这种写法叫做maxLen。
-
-假设dfs的返回值是包含当前节点的最大节点数量,这种写法叫做maxCnt。
-
-大致就是记录的是maxLen而不是maxCnt了,这种比较好写。因为假设在处理前一颗子树的情况时,如果前面是空,因为我们会把maxCnt初始化为1,但是maxCnt如果最小是1就比较奇怪,但是maxLen是0就很合理。
-
-反正在用maxCnt写法写的时候我不太能想清楚,但是用maxLen写法倒是比较好写。
-
-```cpp
-class Solution {
-public:
- // 枚举子集求树的直径
- vector> g;
- vector -
-通过对三角形的边界进行确认,可以加速光栅化的过程,具体代码如下:
-
-```cpp
-//确定bounding box的坐标
-int left = std::min(v[0][0],std::min(v[1][0],v[2][0]));
-int bottom = std::min(v[0][1],std::min(v[1][1],v[2][1]));
-int right = std::max(v[0][0],std::max(v[1][0],v[2][0])) + 1 ; //向上取整
-int top = std::max(v[0][1],std::max(v[1][1],v[2][1])) + 1;
-```
-
-
-
-### 3. 深度buffer
-
-代码中维护了一个**depth_buf**,如果当前要绘制的像素离摄像机近,那么才绘制,否则不绘制。具体的相关代码也很简单:
-
-```cpp
-int index = get_index(x,y);
-if(z_interpolated < depth_buf[index] ){ // if near
- Eigen::Vector3f point;
- point << x,y,z_interpolated;
- Eigen::Vector3f color;
- set_pixel(point,t.getColor());
- depth_buf[index] = z_interpolated;
-}
-```
-
diff --git a/CG/GAMES101/assignment3.md b/CG/GAMES101/assignment3.md
deleted file mode 100644
index bbc0c81..0000000
--- a/CG/GAMES101/assignment3.md
+++ /dev/null
@@ -1,150 +0,0 @@
----
-title: GAMES101-assignment3-Blinn-Phongf以及Shader
-date: 2022-01-01
-tags: [GAMES101]
----
-# Assignment3
-
-两个月没更新了,来填个坑
-
-## 1. 运行结果
-
-这里就贴一个texture shader运行的结果:
-
-
-
-通过对三角形的边界进行确认,可以加速光栅化的过程,具体代码如下:
-
-```cpp
-//确定bounding box的坐标
-int left = std::min(v[0][0],std::min(v[1][0],v[2][0]));
-int bottom = std::min(v[0][1],std::min(v[1][1],v[2][1]));
-int right = std::max(v[0][0],std::max(v[1][0],v[2][0])) + 1 ; //向上取整
-int top = std::max(v[0][1],std::max(v[1][1],v[2][1])) + 1;
-```
-
-
-
-### 3. 深度buffer
-
-代码中维护了一个**depth_buf**,如果当前要绘制的像素离摄像机近,那么才绘制,否则不绘制。具体的相关代码也很简单:
-
-```cpp
-int index = get_index(x,y);
-if(z_interpolated < depth_buf[index] ){ // if near
- Eigen::Vector3f point;
- point << x,y,z_interpolated;
- Eigen::Vector3f color;
- set_pixel(point,t.getColor());
- depth_buf[index] = z_interpolated;
-}
-```
-
diff --git a/CG/GAMES101/assignment3.md b/CG/GAMES101/assignment3.md
deleted file mode 100644
index bbc0c81..0000000
--- a/CG/GAMES101/assignment3.md
+++ /dev/null
@@ -1,150 +0,0 @@
----
-title: GAMES101-assignment3-Blinn-Phongf以及Shader
-date: 2022-01-01
-tags: [GAMES101]
----
-# Assignment3
-
-两个月没更新了,来填个坑
-
-## 1. 运行结果
-
-这里就贴一个texture shader运行的结果:
-
- -
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-个人认为这次作业的主要有三个:
-
-1. 重心插值算法
-2. Blinn-Phong 光照模型
-3. shader以及texture的相关设计
-
-
-
-### 2.1 重心插值算法
-
-这个其实没啥好说的,代码是现成的,就是在 `rasterizer.cpp` 里的 `computeBarycentric2D` 函数,最后返回的是三个值,对应三个顶点的权重。
-
-```cpp
-static std::tuple
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-个人认为这次作业的主要有三个:
-
-1. 重心插值算法
-2. Blinn-Phong 光照模型
-3. shader以及texture的相关设计
-
-
-
-### 2.1 重心插值算法
-
-这个其实没啥好说的,代码是现成的,就是在 `rasterizer.cpp` 里的 `computeBarycentric2D` 函数,最后返回的是三个值,对应三个顶点的权重。
-
-```cpp
-static std::tuple -
-* Blinn-Phong
-
-
-
-* Blinn-Phong
-
-  -
-* texture
-
-
-
-* texture
-
-  -
-* bump
-
-
-
-* bump
-
-  -
-* displacement
-
-
-
-* displacement
-
-  -
-
-
diff --git a/CG/GAMES101/assignment4.md b/CG/GAMES101/assignment4.md
deleted file mode 100644
index 2cb0c1e..0000000
--- a/CG/GAMES101/assignment4.md
+++ /dev/null
@@ -1,48 +0,0 @@
----
-title: GAMES101-assignment4-贝塞尔曲线
-date: 2022-02-28
-tags: [GAMES101]
----
-# Assignment4
-
-## 1. 运行结果
-
-运行结果:
-
-
-
-
-
diff --git a/CG/GAMES101/assignment4.md b/CG/GAMES101/assignment4.md
deleted file mode 100644
index 2cb0c1e..0000000
--- a/CG/GAMES101/assignment4.md
+++ /dev/null
@@ -1,48 +0,0 @@
----
-title: GAMES101-assignment4-贝塞尔曲线
-date: 2022-02-28
-tags: [GAMES101]
----
-# Assignment4
-
-## 1. 运行结果
-
-运行结果:
-
- -
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业比较简单,写一个递归程序就能实现功能,具体如下所示:
-
-```cpp
-cv::Point2f recursive_bezier(const std::vector
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业比较简单,写一个递归程序就能实现功能,具体如下所示:
-
-```cpp
-cv::Point2f recursive_bezier(const std::vector -
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业主要是为了实现光线追踪里的与三角形相交,主要为了实现了两个功能:
-
-1. 实现遍历每个像素,从每个像素发射出光线。
-2. 实现对于光线与三角形相交的判断。
-
-
-
-## 2.1 遍历像素发射光线
-
-这里要实现的目标就是遍历每一个像素,对于每一个像素计算出一个 `dir` 向量,来表示一个当前像素的方向向量。
-
-具体的代码如下所示:
-
-```cpp
-float scale = std::tan(deg2rad(scene.fov * 0.5f));
-float imageAspectRatio = scene.width / (float)scene.height; //宽高比
-
-// Use this variable as the eye position to start your rays.
-Vector3f eye_pos(0);
-int m = 0;
-for (int j = 0; j < scene.height; ++j)
-{
- for (int i = 0; i < scene.width; ++i)
- {
- // generate primary ray direction
- // TODO: Find the x and y positions of the current pixel to get the direction
- // vector that passes through it.
- // Also, don't forget to multiply both of them with the variable *scale*, and
- // x (horizontal) variable with the *imageAspectRatio*
- float x = (((i + 0.5)/scene.width)*2 - 1) * scale * imageAspectRatio;
- float y = (1 - ((j + 0.5)/scene.height)*2) * scale;
- Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
- framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
- }
- UpdateProgress(j / (float)scene.height);
-}
-```
-
-这里需要注意一下**坐标的空间变换**(详细的描述可以见[计算机图形学学习笔记——Whitted-Style Ray Tracing(GAMES101作业5讲解)_dong89801033的博客-CSDN博客](https://blog.csdn.net/dong89801033/article/details/114834898?ops_request_misc=%7B%22request%5Fid%22%3A%22162216944616780357298394%22%2C%22scm%22%3A%2220140713.130102334.pc%5Fall.%22%7D&request_id=162216944616780357298394&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-2-114834898.pc_search_result_cache&utm_term=games101作业5&spm=1018.2226.3001.4187)),这里一共经历了四次变换,分别是:
-
-1. Raster space -> NDC space,把坐标归一化到(0,1)
-
- $$
- x = (i+0.5)/width
- $$
-
- $$
- y = (j+0.5)/height
- $$
-
- 其中,加的0.5是为了保持在像素中心。
-
-2. NDC space -> Screen space, 把坐标映射到(-1,1)
-
- $$
- x = 2*x - 1
- $$
-
- $$
- y = 1 - 2*y
- $$
-
- 这里需要注意一下,y的计算是 1-2*y,原因和坐标的正负有关,因为在原本的NDC space中,y的坐标是向下 为正,然而在Screen Space里,y的坐标是向上为正,所以需要取个符号,不然图像会颠倒。
-
-3. 图像缩放
-
- 因为x和y在进行归一化时,是各自被归一化到了(0,1),因此比例会变得不一样。为了保持图像比例正确,需要为横向乘上一个宽高比。
-
- $$
- x = x * width / height
- $$
-
-4. 关于可视角度
-
- 一般来说,摄像机(eye pos)和成像平面的距离为1,所以我们可以通过控制一个可视角度α来决定能够看到的东西的多少。例如,当α为90°时,tan(2/α) = 1, 也就是说可视角度为[-1,1]。
-
- 所以,这里我们需要为每一个轴来乘上一个scale。
-
- $$
- x = x*tan(\alpha/2)
- $$
-
- $$
- y = x*tan(\alpha/2)
- $$
-
-
-
-最后得到的坐标变化就是:
-
-```cpp
-float x = (((i + 0.5)/scene.width)*2 - 1) * scale * imageAspectRatio;
-float y = (1 - ((j + 0.5)/scene.height)*2) * scale;
-```
-
-
-
-## 2.2 光线与三角形相交
-
-这一块的话直接套Möller-Trumbore算法的公式即可:
-
-
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业主要是为了实现光线追踪里的与三角形相交,主要为了实现了两个功能:
-
-1. 实现遍历每个像素,从每个像素发射出光线。
-2. 实现对于光线与三角形相交的判断。
-
-
-
-## 2.1 遍历像素发射光线
-
-这里要实现的目标就是遍历每一个像素,对于每一个像素计算出一个 `dir` 向量,来表示一个当前像素的方向向量。
-
-具体的代码如下所示:
-
-```cpp
-float scale = std::tan(deg2rad(scene.fov * 0.5f));
-float imageAspectRatio = scene.width / (float)scene.height; //宽高比
-
-// Use this variable as the eye position to start your rays.
-Vector3f eye_pos(0);
-int m = 0;
-for (int j = 0; j < scene.height; ++j)
-{
- for (int i = 0; i < scene.width; ++i)
- {
- // generate primary ray direction
- // TODO: Find the x and y positions of the current pixel to get the direction
- // vector that passes through it.
- // Also, don't forget to multiply both of them with the variable *scale*, and
- // x (horizontal) variable with the *imageAspectRatio*
- float x = (((i + 0.5)/scene.width)*2 - 1) * scale * imageAspectRatio;
- float y = (1 - ((j + 0.5)/scene.height)*2) * scale;
- Vector3f dir = Vector3f(x, y, -1); // Don't forget to normalize this direction!
- framebuffer[m++] = castRay(eye_pos, dir, scene, 0);
- }
- UpdateProgress(j / (float)scene.height);
-}
-```
-
-这里需要注意一下**坐标的空间变换**(详细的描述可以见[计算机图形学学习笔记——Whitted-Style Ray Tracing(GAMES101作业5讲解)_dong89801033的博客-CSDN博客](https://blog.csdn.net/dong89801033/article/details/114834898?ops_request_misc=%7B%22request%5Fid%22%3A%22162216944616780357298394%22%2C%22scm%22%3A%2220140713.130102334.pc%5Fall.%22%7D&request_id=162216944616780357298394&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-2-114834898.pc_search_result_cache&utm_term=games101作业5&spm=1018.2226.3001.4187)),这里一共经历了四次变换,分别是:
-
-1. Raster space -> NDC space,把坐标归一化到(0,1)
-
- $$
- x = (i+0.5)/width
- $$
-
- $$
- y = (j+0.5)/height
- $$
-
- 其中,加的0.5是为了保持在像素中心。
-
-2. NDC space -> Screen space, 把坐标映射到(-1,1)
-
- $$
- x = 2*x - 1
- $$
-
- $$
- y = 1 - 2*y
- $$
-
- 这里需要注意一下,y的计算是 1-2*y,原因和坐标的正负有关,因为在原本的NDC space中,y的坐标是向下 为正,然而在Screen Space里,y的坐标是向上为正,所以需要取个符号,不然图像会颠倒。
-
-3. 图像缩放
-
- 因为x和y在进行归一化时,是各自被归一化到了(0,1),因此比例会变得不一样。为了保持图像比例正确,需要为横向乘上一个宽高比。
-
- $$
- x = x * width / height
- $$
-
-4. 关于可视角度
-
- 一般来说,摄像机(eye pos)和成像平面的距离为1,所以我们可以通过控制一个可视角度α来决定能够看到的东西的多少。例如,当α为90°时,tan(2/α) = 1, 也就是说可视角度为[-1,1]。
-
- 所以,这里我们需要为每一个轴来乘上一个scale。
-
- $$
- x = x*tan(\alpha/2)
- $$
-
- $$
- y = x*tan(\alpha/2)
- $$
-
-
-
-最后得到的坐标变化就是:
-
-```cpp
-float x = (((i + 0.5)/scene.width)*2 - 1) * scale * imageAspectRatio;
-float y = (1 - ((j + 0.5)/scene.height)*2) * scale;
-```
-
-
-
-## 2.2 光线与三角形相交
-
-这一块的话直接套Möller-Trumbore算法的公式即可:
-
- -
-```cpp
-bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig, const Vector3f& dir, float& tnear, float& u, float& v)
-{
- // TODO: Implement this function that tests whether the triangle
- // that's specified bt v0, v1 and v2 intersects with the ray (whose
- // origin is *orig* and direction is *dir*)
- // Also don't forget to update tnear, u and v.
- Vector3f e1 = v1 - v0;
- Vector3f e2 = v2 - v0;
- Vector3f s = orig - v0;
- Vector3f s1 = crossProduct(dir,e2);
- Vector3f s2 = crossProduct(s,e1);
-
- tnear = dotProduct(s2,e2)/dotProduct(s1,e1);
- u = dotProduct(s1,s)/dotProduct(s1,e1);
- v = dotProduct(s2,dir)/dotProduct(s1,e1);
- if(tnear > 0 && u >=0 && v >=0 && (1-u-v) >=0){
- return true;
- }
- return false;
-}
-```
-
-由于外边在循环里对于每一束光线,要和每一个三角形求交,所以,这里把u,v 以及tnear传出去是为了让外边记录最小的tnear以及u,v来记录和哪一个三角形以及三角形的哪一个地方求交了。
-
-
-
diff --git a/CG/GAMES101/assignment6.md b/CG/GAMES101/assignment6.md
deleted file mode 100644
index a590340..0000000
--- a/CG/GAMES101/assignment6.md
+++ /dev/null
@@ -1,117 +0,0 @@
----
-title: GAMES101-assignment6-光线追踪的加速
-date: 2022-03-07
-tags: [GAMES101]
----
-# Assignment6
-
-光线追踪之BVH加速
-
-## 1. 运行结果
-
-运行结果:
-
-
-
-```cpp
-bool rayTriangleIntersect(const Vector3f& v0, const Vector3f& v1, const Vector3f& v2, const Vector3f& orig, const Vector3f& dir, float& tnear, float& u, float& v)
-{
- // TODO: Implement this function that tests whether the triangle
- // that's specified bt v0, v1 and v2 intersects with the ray (whose
- // origin is *orig* and direction is *dir*)
- // Also don't forget to update tnear, u and v.
- Vector3f e1 = v1 - v0;
- Vector3f e2 = v2 - v0;
- Vector3f s = orig - v0;
- Vector3f s1 = crossProduct(dir,e2);
- Vector3f s2 = crossProduct(s,e1);
-
- tnear = dotProduct(s2,e2)/dotProduct(s1,e1);
- u = dotProduct(s1,s)/dotProduct(s1,e1);
- v = dotProduct(s2,dir)/dotProduct(s1,e1);
- if(tnear > 0 && u >=0 && v >=0 && (1-u-v) >=0){
- return true;
- }
- return false;
-}
-```
-
-由于外边在循环里对于每一束光线,要和每一个三角形求交,所以,这里把u,v 以及tnear传出去是为了让外边记录最小的tnear以及u,v来记录和哪一个三角形以及三角形的哪一个地方求交了。
-
-
-
diff --git a/CG/GAMES101/assignment6.md b/CG/GAMES101/assignment6.md
deleted file mode 100644
index a590340..0000000
--- a/CG/GAMES101/assignment6.md
+++ /dev/null
@@ -1,117 +0,0 @@
----
-title: GAMES101-assignment6-光线追踪的加速
-date: 2022-03-07
-tags: [GAMES101]
----
-# Assignment6
-
-光线追踪之BVH加速
-
-## 1. 运行结果
-
-运行结果:
-
- -
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业使用了BVH来对光线追踪实现了加速,其中有两个地方比较重要:
-
-1. 如何实现光线和**A**xis-**A**ligned **B**ounding **B**ox(AABB)求交。
-2. 如何实现光线和BVH的一个node求交。
-
-
-
-## 2.1 光线与AABB求交
-
-这个的具体做法在GAMES101课程里已经讲的很清楚了:
-
-使用六个平面来定义出一个box:
-
-
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业使用了BVH来对光线追踪实现了加速,其中有两个地方比较重要:
-
-1. 如何实现光线和**A**xis-**A**ligned **B**ounding **B**ox(AABB)求交。
-2. 如何实现光线和BVH的一个node求交。
-
-
-
-## 2.1 光线与AABB求交
-
-这个的具体做法在GAMES101课程里已经讲的很清楚了:
-
-使用六个平面来定义出一个box:
-
- -
-然后计算光线与这六个平面相交的时间,因为是axis-aligned的,所以可以采用正视图/侧视图/俯视图的方式来简易计算求交的时间。
-
-
-
-然后计算光线与这六个平面相交的时间,因为是axis-aligned的,所以可以采用正视图/侧视图/俯视图的方式来简易计算求交的时间。
-
- -
-对于每一个axis,可以计算出两个平面的求交时间分别为t_min和t_max,于是最后我们可以得到三组t_min, t_max。
-
-最后取一个交集,就能够计算出光线进入这个box的t_min, t_max:
-
-
-
-对于每一个axis,可以计算出两个平面的求交时间分别为t_min和t_max,于是最后我们可以得到三组t_min, t_max。
-
-最后取一个交集,就能够计算出光线进入这个box的t_min, t_max:
-
-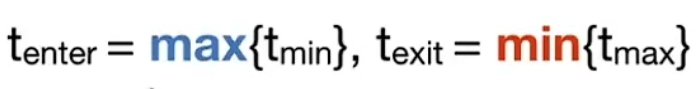 -
-具体的代码如下所示:
-
-```python
-inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
- const std::array
-
-具体的代码如下所示:
-
-```python
-inline bool Bounds3::IntersectP(const Ray& ray, const Vector3f& invDir,
- const std::array -
-
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业主要实现了路径追踪,其中涉及到的坑点比较多,主要是以下几个:
-
-1. 相较于assignment6有几个地方需要修改一下,不然会出现**很错误的结果**。
-2. 直接光照的实现
-3. 间接光照的实现
-4. 还可以拓展的地方
-
-
-
-## 2.1 在assignment6的基础上修改(注意)
-
-首先,需要对 `BVH.cpp` 的 `BVHAccel::getIntersection` 函数进行修改:
-
-```cpp
-std::array
-
-
-
-## 2. 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-这次作业主要实现了路径追踪,其中涉及到的坑点比较多,主要是以下几个:
-
-1. 相较于assignment6有几个地方需要修改一下,不然会出现**很错误的结果**。
-2. 直接光照的实现
-3. 间接光照的实现
-4. 还可以拓展的地方
-
-
-
-## 2.1 在assignment6的基础上修改(注意)
-
-首先,需要对 `BVH.cpp` 的 `BVHAccel::getIntersection` 函数进行修改:
-
-```cpp
-std::array -
-* spp = 16
-
-
-
-* spp = 16
-
-  -
-* spp = 32
-
-
-
-* spp = 32
-
-  -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
diff --git a/CG/GAMES202/README.md b/CG/GAMES202/README.md
deleted file mode 100644
index 3e7a4d3..0000000
--- a/CG/GAMES202/README.md
+++ /dev/null
@@ -1,3 +0,0 @@
-这里会整理GAMES202的各个assignments的代码以及相关的知识
-
-* [Assignment1](assignment1.md)
diff --git a/CG/GAMES202/assignment1.md b/CG/GAMES202/assignment1.md
deleted file mode 100644
index 8164000..0000000
--- a/CG/GAMES202/assignment1.md
+++ /dev/null
@@ -1,185 +0,0 @@
----
-title: GAMES202-Assinment1-实时阴影
-date: 2022-04-09
-tags: [GAMES202]
----
-> 日期:2022.4.11
-
-# Assignment1-实时阴影
-
-开始看games202了,第一次的作业是实时阴影,参考了一些GitHub的代码然后自己实现了一下,虽然感觉还有不少的问题...
-
-## 运行结果
-
-这里贴一个pcss的运行结果,感觉看起来不太对。。。
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
diff --git a/CG/GAMES202/README.md b/CG/GAMES202/README.md
deleted file mode 100644
index 3e7a4d3..0000000
--- a/CG/GAMES202/README.md
+++ /dev/null
@@ -1,3 +0,0 @@
-这里会整理GAMES202的各个assignments的代码以及相关的知识
-
-* [Assignment1](assignment1.md)
diff --git a/CG/GAMES202/assignment1.md b/CG/GAMES202/assignment1.md
deleted file mode 100644
index 8164000..0000000
--- a/CG/GAMES202/assignment1.md
+++ /dev/null
@@ -1,185 +0,0 @@
----
-title: GAMES202-Assinment1-实时阴影
-date: 2022-04-09
-tags: [GAMES202]
----
-> 日期:2022.4.11
-
-# Assignment1-实时阴影
-
-开始看games202了,第一次的作业是实时阴影,参考了一些GitHub的代码然后自己实现了一下,虽然感觉还有不少的问题...
-
-## 运行结果
-
-这里贴一个pcss的运行结果,感觉看起来不太对。。。
-
- -
-## 实现细节
-
-### 0. 坐标转换
-
-首先,在写shader之前,需要缕清楚坐标的变换,比如说这里,在真正开始进行深度测试之前,你需要得到shadowmap上真正对应的坐标,也就是**从光源的角度看过去的一个转化为了ndc的坐标**。
-
-那么就需要做两步:
-
-1. 坐标变换,把世界坐标系下(?)转换到从光源角度看过去的坐标。
-2. ndc变化
-
-具体的实现就是:
-
-```glsl
-// 坐标变换,在vertex shader里
-vPositionFromLight = uLightMVP * vec4(aVertexPosition, 1.0);
-
-// ndc变换,在fragment shader里
-vec3 shadowCoord = (vPositionFromLight.xyz / vPositionFromLight.w) * 0.5 + 0.5; //为啥是 *0.5 + 0.5 ? ...
-```
-
-这里的`*0.5 + 0.5` 我比较迷惑(我抄的github),根据我的理解,前面的`(vPositionFromLight.xyz / vPositionFromLight.w)`是做一个归一化,那么后面的`*0.5 + 0.5`应该就是一个平移的操作,但是我觉得具体乘多少加多少要根据数据的范围来定。
-
-> 我猜测进行了`(vPositionFromLight.xyz / vPositionFromLight.w)`的数据范围在 [-1,1],这样的话[-1\*0.5 + 0.5, 1\*0.5+0.5] 刚好就被shift到了[0,1]。。。
-
-
-
-### 1. 硬阴影
-
-既然得到了以光源为原点的坐标系的坐标,那么做硬阴影就很简单了,代码如下:
-
-```glsl
-// 直接使用shadowMap产生硬阴影
-float useShadowMap(sampler2D shadowMap, vec4 shadowCoord){
- // 使用shadowCoord在shadowMap采样获得深度值,然后与实际的z进行比较
- vec4 depthPack = texture2D(shadowMap, shadowCoord.xy); //因为从深度图中查询到的实际上是一个颜色
- float depth = unpack(depthPack); //所以在这里需要把深度图查询到的颜色转换为一个浮点数
- if(depth < shadowCoord.z){
- return 0.0;
- }
- return 1.0;
-}
-```
-
-思路就是在shadowMap里去查那个点的深度,然后与实际的深度比,如果实际的深度更大,那么就没挡住,否则就挡住了。
-
-需要稍微注意的是`unpack`操作,因为深度图实际上是一张图片,所以需要将那个点的rgba像素转换为浮点数后才能进行比较。
-
-使用硬阴影的效果图如下:
-
-
-
-## 实现细节
-
-### 0. 坐标转换
-
-首先,在写shader之前,需要缕清楚坐标的变换,比如说这里,在真正开始进行深度测试之前,你需要得到shadowmap上真正对应的坐标,也就是**从光源的角度看过去的一个转化为了ndc的坐标**。
-
-那么就需要做两步:
-
-1. 坐标变换,把世界坐标系下(?)转换到从光源角度看过去的坐标。
-2. ndc变化
-
-具体的实现就是:
-
-```glsl
-// 坐标变换,在vertex shader里
-vPositionFromLight = uLightMVP * vec4(aVertexPosition, 1.0);
-
-// ndc变换,在fragment shader里
-vec3 shadowCoord = (vPositionFromLight.xyz / vPositionFromLight.w) * 0.5 + 0.5; //为啥是 *0.5 + 0.5 ? ...
-```
-
-这里的`*0.5 + 0.5` 我比较迷惑(我抄的github),根据我的理解,前面的`(vPositionFromLight.xyz / vPositionFromLight.w)`是做一个归一化,那么后面的`*0.5 + 0.5`应该就是一个平移的操作,但是我觉得具体乘多少加多少要根据数据的范围来定。
-
-> 我猜测进行了`(vPositionFromLight.xyz / vPositionFromLight.w)`的数据范围在 [-1,1],这样的话[-1\*0.5 + 0.5, 1\*0.5+0.5] 刚好就被shift到了[0,1]。。。
-
-
-
-### 1. 硬阴影
-
-既然得到了以光源为原点的坐标系的坐标,那么做硬阴影就很简单了,代码如下:
-
-```glsl
-// 直接使用shadowMap产生硬阴影
-float useShadowMap(sampler2D shadowMap, vec4 shadowCoord){
- // 使用shadowCoord在shadowMap采样获得深度值,然后与实际的z进行比较
- vec4 depthPack = texture2D(shadowMap, shadowCoord.xy); //因为从深度图中查询到的实际上是一个颜色
- float depth = unpack(depthPack); //所以在这里需要把深度图查询到的颜色转换为一个浮点数
- if(depth < shadowCoord.z){
- return 0.0;
- }
- return 1.0;
-}
-```
-
-思路就是在shadowMap里去查那个点的深度,然后与实际的深度比,如果实际的深度更大,那么就没挡住,否则就挡住了。
-
-需要稍微注意的是`unpack`操作,因为深度图实际上是一张图片,所以需要将那个点的rgba像素转换为浮点数后才能进行比较。
-
-使用硬阴影的效果图如下:
-
- -
-### 2. PCF
-
-PCF思想也很简单,就是在自己周围做一个采样,然后看有多少物体被挡住(1),有多少没被挡住(0),然后做一个平均来表示自身的visibility。
-
-作业给出的框架是使用了均匀采样和泊松采样,比如说像这样:
-
-```glsl
-void poissonDiskSamples( const in vec2 randomSeed ) {
-
- float ANGLE_STEP = PI2 * float( NUM_RINGS ) / float( NUM_SAMPLES );
- float INV_NUM_SAMPLES = 1.0 / float( NUM_SAMPLES );
-
- float angle = rand_2to1( randomSeed ) * PI2;
- float radius = INV_NUM_SAMPLES;
- float radiusStep = radius;
-
- for( int i = 0; i < NUM_SAMPLES; i ++ ) {
- poissonDisk[i] = vec2( cos( angle ), sin( angle ) ) * pow( radius, 0.75 );
- radius += radiusStep;
- angle += ANGLE_STEP;
- }
-}
-```
-
-我们只需要给它穿入一个seed,然后就可以通过访问`poissonDisk[i]`去得到一个采样后的值,不过我有点没太搞懂这个得到的采样后的值的一个大致范围,我只知道它是均匀的,所以后面我就开始瞎搞了。
-
-PCF的代码大致如下:
-
-```glsl
-float PCF(sampler2D shadowMap, vec4 coords, float filterSize) {
- uniformDiskSamples(coords.xy);
- // poissonDiskSamples(coords.xy);
- float ans = 0.0;
- // 其实这个值应该是有一个具体含义,然后计算出来的,不过不太清楚poissonDisk里的值的一个具体范围,所以就随便设了。
- for(int i=0;i
-
-### 2. PCF
-
-PCF思想也很简单,就是在自己周围做一个采样,然后看有多少物体被挡住(1),有多少没被挡住(0),然后做一个平均来表示自身的visibility。
-
-作业给出的框架是使用了均匀采样和泊松采样,比如说像这样:
-
-```glsl
-void poissonDiskSamples( const in vec2 randomSeed ) {
-
- float ANGLE_STEP = PI2 * float( NUM_RINGS ) / float( NUM_SAMPLES );
- float INV_NUM_SAMPLES = 1.0 / float( NUM_SAMPLES );
-
- float angle = rand_2to1( randomSeed ) * PI2;
- float radius = INV_NUM_SAMPLES;
- float radiusStep = radius;
-
- for( int i = 0; i < NUM_SAMPLES; i ++ ) {
- poissonDisk[i] = vec2( cos( angle ), sin( angle ) ) * pow( radius, 0.75 );
- radius += radiusStep;
- angle += ANGLE_STEP;
- }
-}
-```
-
-我们只需要给它穿入一个seed,然后就可以通过访问`poissonDisk[i]`去得到一个采样后的值,不过我有点没太搞懂这个得到的采样后的值的一个大致范围,我只知道它是均匀的,所以后面我就开始瞎搞了。
-
-PCF的代码大致如下:
-
-```glsl
-float PCF(sampler2D shadowMap, vec4 coords, float filterSize) {
- uniformDiskSamples(coords.xy);
- // poissonDiskSamples(coords.xy);
- float ans = 0.0;
- // 其实这个值应该是有一个具体含义,然后计算出来的,不过不太清楚poissonDisk里的值的一个具体范围,所以就随便设了。
- for(int i=0;i -
-
-
-### 3. PCSS
-
-PCSS就是估计一个平均的blocker depth后去求一个半影长度,后面就和PCF一模一样了。
-
-首先是求平均的blocker depth,大概长这样:
-
-```glsl
-float findBlocker( sampler2D shadowMap, vec2 uv, float zReceiver ) {
- uniformDiskSamples(uv); //采样
- float allDepth = 0.0;
- int blockerCnt = 0;
- for(int i=0;i
-
-
-
-### 3. PCSS
-
-PCSS就是估计一个平均的blocker depth后去求一个半影长度,后面就和PCF一模一样了。
-
-首先是求平均的blocker depth,大概长这样:
-
-```glsl
-float findBlocker( sampler2D shadowMap, vec2 uv, float zReceiver ) {
- uniformDiskSamples(uv); //采样
- float allDepth = 0.0;
- int blockerCnt = 0;
- for(int i=0;i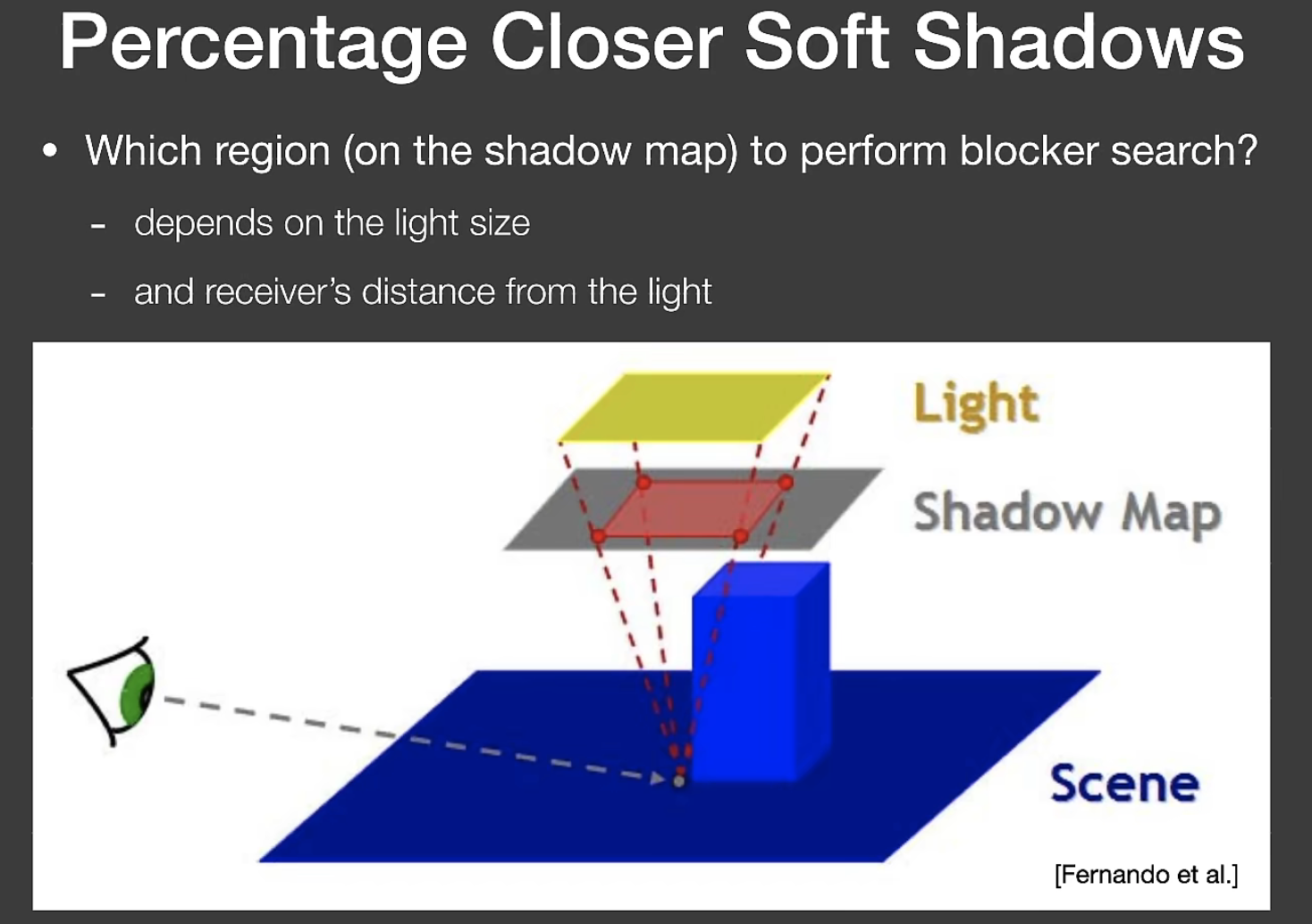 -
-不过我没有用这种方法(抱歉),我又直接设了一个 `BLOCKER_SIZE = 0.01`,可能就是这个原因让后面的结果看起来很怪。
-
-求出了 blocker depth 后,再算一个半影长度(把半影长度当成一个filter size),最后就可以直接套PCF了,代码大致如下:
-
-```glsl
-float PCSS(sampler2D shadowMap, vec4 coords){
-
- // STEP 1: avgblocker depth
- float averageDepth = findBlocker(shadowMap, coords.xy, coords.z);
-
- // STEP 2: penumbra size
- // 使用相似三角形计算半影
- float dReceiver = coords.z;
- float dBlocker = averageDepth;
- float penumbraSize = float(L_WIDTH) * (dReceiver - dBlocker)/ dBlocker * 0.01;
- // STEP 3: filtering
- return PCF(shadowMap, coords, penumbraSize);
-}
-```
-
-关于使用相似三角形计算半影的图长这样:
-
-
-
-不过我没有用这种方法(抱歉),我又直接设了一个 `BLOCKER_SIZE = 0.01`,可能就是这个原因让后面的结果看起来很怪。
-
-求出了 blocker depth 后,再算一个半影长度(把半影长度当成一个filter size),最后就可以直接套PCF了,代码大致如下:
-
-```glsl
-float PCSS(sampler2D shadowMap, vec4 coords){
-
- // STEP 1: avgblocker depth
- float averageDepth = findBlocker(shadowMap, coords.xy, coords.z);
-
- // STEP 2: penumbra size
- // 使用相似三角形计算半影
- float dReceiver = coords.z;
- float dBlocker = averageDepth;
- float penumbraSize = float(L_WIDTH) * (dReceiver - dBlocker)/ dBlocker * 0.01;
- // STEP 3: filtering
- return PCF(shadowMap, coords, penumbraSize);
-}
-```
-
-关于使用相似三角形计算半影的图长这样:
-
-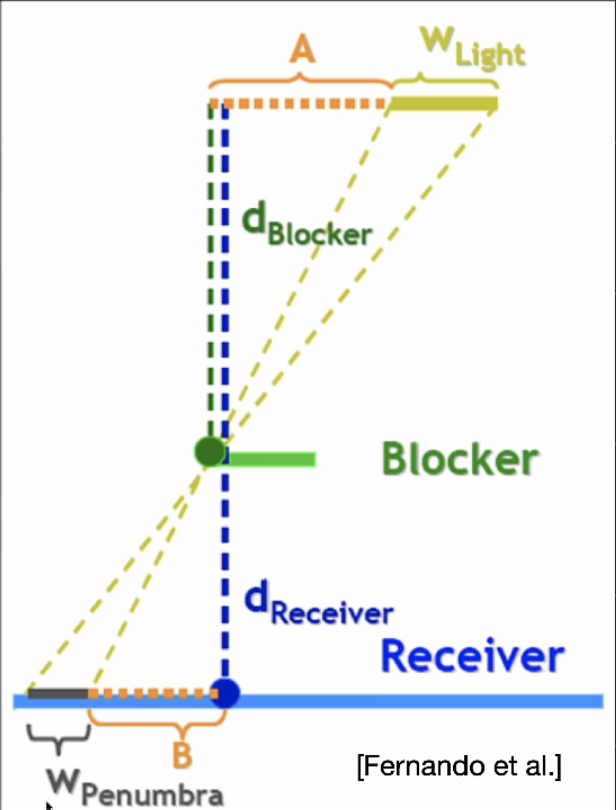 -
-至于为什么我在算半影时后面又乘了一个0.01,是因为不乘0.01范围又大了。。就把这个0.01当成filter_size吧。
-
-最后PCSS的结果如下:
-
-> 这肯定不对,可能还是算平均blocker depth那里有问题🤔,这里的图是 BLOCKER_DPETH 为0.01的结果,随着把BLOCKER_DPETH变大,实的影子的长度会越来越短,0.05~0.08时效果还行,但是都是野路子。。。
-
-
-
-至于为什么我在算半影时后面又乘了一个0.01,是因为不乘0.01范围又大了。。就把这个0.01当成filter_size吧。
-
-最后PCSS的结果如下:
-
-> 这肯定不对,可能还是算平均blocker depth那里有问题🤔,这里的图是 BLOCKER_DPETH 为0.01的结果,随着把BLOCKER_DPETH变大,实的影子的长度会越来越短,0.05~0.08时效果还行,但是都是野路子。。。
-
- -
-
-
-## 总结
-
-感觉这次做的太糙了,但是也不想做了,暂时先这样,写shader太坐牢了,连print都不能打,调试地狱。所以我还是不知道到底采样后的数组里的数据范围是多少,这也是我在使用万能的0.01的原因。
-
-
-
diff --git a/CG/OpenGL/README.md b/CG/OpenGL/README.md
deleted file mode 100644
index 99406c1..0000000
--- a/CG/OpenGL/README.md
+++ /dev/null
@@ -1,2 +0,0 @@
-记录在opengl下踩的坑
-* [如何使用assimp读取没有贴图的obj模型](assimp_material.md)
\ No newline at end of file
diff --git a/CG/OpenGL/assimp_material.md b/CG/OpenGL/assimp_material.md
deleted file mode 100644
index 2528973..0000000
--- a/CG/OpenGL/assimp_material.md
+++ /dev/null
@@ -1,112 +0,0 @@
----
-title: 如何使用assimp读取obj文件的材质
-date: 2022-03-25
-tags: [OpenGL]
----
-> 日期: 2022年3月25日
-
-
-
-# 如何使用assimp读取obj文件的材质
-
-之前在看LearnOpenGL的[这一节](https://learnopengl-cn.github.io/03 Model Loading/03 Model/),主要讲的就是使用assimp来加载模型,但是给的参考代码只针对了模型有材质贴图的情况,也就是通过去获取diffuse贴图以及specular贴图的方式获得模型的材质。
-
-比如这是官方给的示例的文件,其中包含了很多的材质贴图:
-
-
-
-
-
-## 总结
-
-感觉这次做的太糙了,但是也不想做了,暂时先这样,写shader太坐牢了,连print都不能打,调试地狱。所以我还是不知道到底采样后的数组里的数据范围是多少,这也是我在使用万能的0.01的原因。
-
-
-
diff --git a/CG/OpenGL/README.md b/CG/OpenGL/README.md
deleted file mode 100644
index 99406c1..0000000
--- a/CG/OpenGL/README.md
+++ /dev/null
@@ -1,2 +0,0 @@
-记录在opengl下踩的坑
-* [如何使用assimp读取没有贴图的obj模型](assimp_material.md)
\ No newline at end of file
diff --git a/CG/OpenGL/assimp_material.md b/CG/OpenGL/assimp_material.md
deleted file mode 100644
index 2528973..0000000
--- a/CG/OpenGL/assimp_material.md
+++ /dev/null
@@ -1,112 +0,0 @@
----
-title: 如何使用assimp读取obj文件的材质
-date: 2022-03-25
-tags: [OpenGL]
----
-> 日期: 2022年3月25日
-
-
-
-# 如何使用assimp读取obj文件的材质
-
-之前在看LearnOpenGL的[这一节](https://learnopengl-cn.github.io/03 Model Loading/03 Model/),主要讲的就是使用assimp来加载模型,但是给的参考代码只针对了模型有材质贴图的情况,也就是通过去获取diffuse贴图以及specular贴图的方式获得模型的材质。
-
-比如这是官方给的示例的文件,其中包含了很多的材质贴图:
-
- -
-在相关的mtl文件里也链接到了具体的贴图文件:
-
-
-
-在相关的mtl文件里也链接到了具体的贴图文件:
-
- -
-但是我们在使用blender等很多软件建模时是没有材质贴图的,一般来说只有一个obj文件和一个mtl文件:
-
-
-
-但是我们在使用blender等很多软件建模时是没有材质贴图的,一般来说只有一个obj文件和一个mtl文件:
-
- -
-
-
- -
-所以只要想办法获取到mtl文件里的Ka, Kd, Ks这几项,然后想办法把它传进shader渲染就行了。
-
-
-
-首先,使用assimp来获取这几个值的核心代码在这里:
-
-```cpp
-Material loadMaterialWithoutTextures(aiMaterial *mat){
- Material result;
- aiColor3D color;
- //读取mtl文件顶点数据
- mat->Get(AI_MATKEY_COLOR_AMBIENT, color);
- result.ambient = glm::vec3(color.r, color.g, color.b);
- mat->Get(AI_MATKEY_COLOR_DIFFUSE, color);
- result.diffuse = glm::vec3(color.r, color.g, color.b);
- mat->Get(AI_MATKEY_COLOR_SPECULAR, color);
- result.specular = glm::vec3(color.r, color.g, color.b);
- return result;
- }
-```
-
-需要进行一些判断来这个mesh是否是拥有材质贴图的mesh,如果没有材质贴图,就去读取Ka, Kd, Ks,否则就直接去读取贴图(原本的实现方法)。
-
-```cpp
-if(material->GetTextureCount(aiTextureType_DIFFUSE) == 0 && material->GetTextureCount(aiTextureType_SPECULAR) == 0){
- //没有贴图,之前读取模型的material的值
- Material colorMaterial = loadMaterialWithoutTextures(material);
- return Mesh(vertices, indices, colorMaterial);
- }
- else{
- vector
-
-所以只要想办法获取到mtl文件里的Ka, Kd, Ks这几项,然后想办法把它传进shader渲染就行了。
-
-
-
-首先,使用assimp来获取这几个值的核心代码在这里:
-
-```cpp
-Material loadMaterialWithoutTextures(aiMaterial *mat){
- Material result;
- aiColor3D color;
- //读取mtl文件顶点数据
- mat->Get(AI_MATKEY_COLOR_AMBIENT, color);
- result.ambient = glm::vec3(color.r, color.g, color.b);
- mat->Get(AI_MATKEY_COLOR_DIFFUSE, color);
- result.diffuse = glm::vec3(color.r, color.g, color.b);
- mat->Get(AI_MATKEY_COLOR_SPECULAR, color);
- result.specular = glm::vec3(color.r, color.g, color.b);
- return result;
- }
-```
-
-需要进行一些判断来这个mesh是否是拥有材质贴图的mesh,如果没有材质贴图,就去读取Ka, Kd, Ks,否则就直接去读取贴图(原本的实现方法)。
-
-```cpp
-if(material->GetTextureCount(aiTextureType_DIFFUSE) == 0 && material->GetTextureCount(aiTextureType_SPECULAR) == 0){
- //没有贴图,之前读取模型的material的值
- Material colorMaterial = loadMaterialWithoutTextures(material);
- return Mesh(vertices, indices, colorMaterial);
- }
- else{
- vector diff --git a/CG/README.md b/CG/README.md
deleted file mode 100644
index ce08f91..0000000
--- a/CG/README.md
+++ /dev/null
@@ -1,2 +0,0 @@
-这里会整理一些关于计算机图形学的知识。
-* [GAMES101 assignments](GAMES101/README.md)
\ No newline at end of file
diff --git a/CG/SoftRasterizer/3d.md b/CG/SoftRasterizer/3d.md
deleted file mode 100644
index b50cca5..0000000
--- a/CG/SoftRasterizer/3d.md
+++ /dev/null
@@ -1,232 +0,0 @@
----
-title: 软光栅器MicroRenderer(二) 进入三维
-date: 2022-05-27 23:38:00
-tags: [MicroRenderer]
----
-# 软光栅器MicroRenderer(二) 进入三维
-代码见:https://github.com/LJHG/MicroRenderer
-
-本次主要讨论的内容是 mvp变换,三角形的裁切以及相机控制。
-
-## 1. mvp变换
-
-具体的mvp矩阵推导这里就不细讲了,关于mvp变换我基本上是参照了games101课程里的内容,可以看一下这里:[Assignment1 · GitBook (ljhblog.top)](https://www.ljhblog.top/CG/GAMES101/assignment1.html) 。其中我的view matrix 和 projection matrix 是完全按照课程上的描述实现的,不过最后的我的视图矩阵和透视矩阵好像实现出来好像都有点问题。。。所以目前我的这两个矩阵都是抄的[别人的](https://yangwc.com/2019/05/01/SoftRenderer-Math/),暂时还没啥问题。
-
-一旦你会计算mvp矩阵了,剩下的事情就很简单了,只需要去继承Shader然后实现一个新的类,并且把vertex shader重新实现为三维版本就可以了,在三维空间的shader里,vertex shader的职责就是把顶点进行mvp变换。
-
-```cpp
-// 3d shader, implement mvp transformation for vertex shader, fragment shader just pass color
-class ThreeDShader: public Shader{
-public:
- ThreeDShader(glm::mat4 _modelMatrix, glm::mat4 _viewMatrix, glm::mat4 _projectionMatrix);
- VertexOutData vertexShader(VertexData &v) override;
- glm::vec4 fragmentShader(VertexOutData &v) override;
-};
-```
-
-```cpp
-VertexOutData ThreeDShader::vertexShader(VertexData &v) {
- VertexOutData vod;
- vod.position = glm::vec4(v.position,1.0f);
- vod.position = projectionMatrix * viewMatrix * modelMatrix * vod.position; //mvp transformation
- vod.color= v.color;
- vod.normal = v.normal;
- return vod;
-}
-
-glm::vec4 ThreeDShader::fragmentShader(VertexOutData &v) {
- glm::vec4 result;
- result = v.color;
- return result;
-}
-```
-
-因为不涉及具体的着色,所以这里我们的 fragment shader仍然传递颜色即可。
-
-
-
-## 2. 三角形的裁切
-
-> 究极野路子,谨慎参考
-
-关于三角形的裁切这个东西,一般来说应该是放在光栅化之前来做:[渲染管线中,背面剔除和齐次空间的裁剪哪个先进行?为什么? - 知乎 (zhihu.com)](https://www.zhihu.com/question/469259481/answer/1973677886)。裁切有很多很复杂的算法。一般来说,大家会把三角形裁切和背面剔除放在一起来讨论。
-
-不过我这里就比较拉了,为了实现最简单的方法,我把裁切放在了光栅化的时候来做。具体的原理就是,通过对经过了视口变换的坐标进行判断,也就是说如果x坐标不在 `[0,width]` 内,y坐标不在 `[0,height]`内,z坐标不在`[-1,1]`内,那么就不去画它。。。
-
-具体的代码就是这样:
-
-```cpp
-void ShadingPipeline::fillRasterization(VertexOutData &v1, VertexOutData &v2, VertexOutData &v3) {
- // I don't know name for this algorithm
- // ref: GAMES101 assignment2: https://www.ljhblog.top/CG/GAMES101/assignment2.html
- float x1 = v1.position[0]; float y1 = v1.position[1]; float z1 = v1.position[2];
- float x2 = v2.position[0]; float y2 = v2.position[1]; float z2 = v2.position[2];
- float x3 = v3.position[0]; float y3 = v3.position[1]; float z3 = v3.position[2];
-
- /**
- * 关于clip是否应该在光栅化时做的问题
- * 一般来说,clip好像应该在做光栅化前来做,但是如果直接在光栅化时做会十分方便...
- * 这里我在光栅化时作了两个clip:
- * 1. 一个判断z,如果z不在[-1,1]内,那么就说明不再视线范围内,直接不画
- * 2. 另一个对left right bottom top 做一个裁剪,不去管屏幕空间外的像素了
- */
- // clip1
- if(z1<-1.0f || z1 >1.0f || z2<-1.0f || z2 > 1.0f || z3<-1.0f || z3>1.0f){
- //out of depth range, clip
- return;
- }
-
- // get bounding box of the triangle
- int left = static_cast
diff --git a/CG/README.md b/CG/README.md
deleted file mode 100644
index ce08f91..0000000
--- a/CG/README.md
+++ /dev/null
@@ -1,2 +0,0 @@
-这里会整理一些关于计算机图形学的知识。
-* [GAMES101 assignments](GAMES101/README.md)
\ No newline at end of file
diff --git a/CG/SoftRasterizer/3d.md b/CG/SoftRasterizer/3d.md
deleted file mode 100644
index b50cca5..0000000
--- a/CG/SoftRasterizer/3d.md
+++ /dev/null
@@ -1,232 +0,0 @@
----
-title: 软光栅器MicroRenderer(二) 进入三维
-date: 2022-05-27 23:38:00
-tags: [MicroRenderer]
----
-# 软光栅器MicroRenderer(二) 进入三维
-代码见:https://github.com/LJHG/MicroRenderer
-
-本次主要讨论的内容是 mvp变换,三角形的裁切以及相机控制。
-
-## 1. mvp变换
-
-具体的mvp矩阵推导这里就不细讲了,关于mvp变换我基本上是参照了games101课程里的内容,可以看一下这里:[Assignment1 · GitBook (ljhblog.top)](https://www.ljhblog.top/CG/GAMES101/assignment1.html) 。其中我的view matrix 和 projection matrix 是完全按照课程上的描述实现的,不过最后的我的视图矩阵和透视矩阵好像实现出来好像都有点问题。。。所以目前我的这两个矩阵都是抄的[别人的](https://yangwc.com/2019/05/01/SoftRenderer-Math/),暂时还没啥问题。
-
-一旦你会计算mvp矩阵了,剩下的事情就很简单了,只需要去继承Shader然后实现一个新的类,并且把vertex shader重新实现为三维版本就可以了,在三维空间的shader里,vertex shader的职责就是把顶点进行mvp变换。
-
-```cpp
-// 3d shader, implement mvp transformation for vertex shader, fragment shader just pass color
-class ThreeDShader: public Shader{
-public:
- ThreeDShader(glm::mat4 _modelMatrix, glm::mat4 _viewMatrix, glm::mat4 _projectionMatrix);
- VertexOutData vertexShader(VertexData &v) override;
- glm::vec4 fragmentShader(VertexOutData &v) override;
-};
-```
-
-```cpp
-VertexOutData ThreeDShader::vertexShader(VertexData &v) {
- VertexOutData vod;
- vod.position = glm::vec4(v.position,1.0f);
- vod.position = projectionMatrix * viewMatrix * modelMatrix * vod.position; //mvp transformation
- vod.color= v.color;
- vod.normal = v.normal;
- return vod;
-}
-
-glm::vec4 ThreeDShader::fragmentShader(VertexOutData &v) {
- glm::vec4 result;
- result = v.color;
- return result;
-}
-```
-
-因为不涉及具体的着色,所以这里我们的 fragment shader仍然传递颜色即可。
-
-
-
-## 2. 三角形的裁切
-
-> 究极野路子,谨慎参考
-
-关于三角形的裁切这个东西,一般来说应该是放在光栅化之前来做:[渲染管线中,背面剔除和齐次空间的裁剪哪个先进行?为什么? - 知乎 (zhihu.com)](https://www.zhihu.com/question/469259481/answer/1973677886)。裁切有很多很复杂的算法。一般来说,大家会把三角形裁切和背面剔除放在一起来讨论。
-
-不过我这里就比较拉了,为了实现最简单的方法,我把裁切放在了光栅化的时候来做。具体的原理就是,通过对经过了视口变换的坐标进行判断,也就是说如果x坐标不在 `[0,width]` 内,y坐标不在 `[0,height]`内,z坐标不在`[-1,1]`内,那么就不去画它。。。
-
-具体的代码就是这样:
-
-```cpp
-void ShadingPipeline::fillRasterization(VertexOutData &v1, VertexOutData &v2, VertexOutData &v3) {
- // I don't know name for this algorithm
- // ref: GAMES101 assignment2: https://www.ljhblog.top/CG/GAMES101/assignment2.html
- float x1 = v1.position[0]; float y1 = v1.position[1]; float z1 = v1.position[2];
- float x2 = v2.position[0]; float y2 = v2.position[1]; float z2 = v2.position[2];
- float x3 = v3.position[0]; float y3 = v3.position[1]; float z3 = v3.position[2];
-
- /**
- * 关于clip是否应该在光栅化时做的问题
- * 一般来说,clip好像应该在做光栅化前来做,但是如果直接在光栅化时做会十分方便...
- * 这里我在光栅化时作了两个clip:
- * 1. 一个判断z,如果z不在[-1,1]内,那么就说明不再视线范围内,直接不画
- * 2. 另一个对left right bottom top 做一个裁剪,不去管屏幕空间外的像素了
- */
- // clip1
- if(z1<-1.0f || z1 >1.0f || z2<-1.0f || z2 > 1.0f || z3<-1.0f || z3>1.0f){
- //out of depth range, clip
- return;
- }
-
- // get bounding box of the triangle
- int left = static_cast -
-
-
-这里大致说一下每一个文件的作用(虽然后续有重构的可能性):
-
-1. CommonUtils.cpp。用来存放一些通用函数,比如说读取图片之类的。
-2. MathUtils.cpp。用来存放数学相关的函数,比如说计算MVP矩阵,插值等。
-3. Renderer.cpp。渲染相关代码,用来管理渲染的物体以及调用渲染管线渲染等。
-4. Shader.cpp。存放shader代码。
-5. ShadingPipeline.cpp。渲染管线代码,生成渲染结果。
-6. Structure.cpp。定义vetex, frament 以及 mesh的数据类型。
-7. WindowApp.cpp。SDL2相关函数。
-
-> 关于Renderer 和ShadingPipeline 以及 Shader 的组织问题:
->
-> 关于这三个类的所属关系大概是:
->
-> ShadingPipeline 是 Renderer的一个成员,同时 Shader 是 Shadingpipeline的一个成员。
->
-> Renderer主要负责管理场景里的Mesh,同时调用Shadingpipeline去渲染。
->
-> ShadingPipeline主要负责渲染管线的一整套流程,比如说根据vertices indices 构建三角形,比如说光栅化。
->
-> Shader主要负责实现自己的vertexShader以及FragmentShader函数。
-
-## 2. 具体细节
-
-### 2.1 像素展示
-
-基本上可以把渲染的整个过程抽离为 生成像素buffer -> 显示像素buffer。显示像素buffer这个部分就交给了SDL2来做,只需要在每一帧的时候把一个像素数组传递给SDL2就可以展示了,所以我们的渲染器所需要的就是在每一帧生成出这个像素数组就可以了。这里的选取是非常随意的,在GAMES101里使用的opencv来把结果存成图片,[这位大佬的博客](https://yangwc.com/2019/05/01/SoftRenderer-Rasterization/)使用了qt来展示结果,后来他后续把代码重构了,也是使用的SDL2。
-
-比如说其实核心就是 `updateCanvas`这个函数:
-
-```cpp
-void WindowApp::updateCanvas(uint8_t* pixels, int width, int height, int channel) {
- SDL_LockSurface(windowSurface);
- Uint32* surfacePixels = (Uint32*)windowSurface->pixels; //获取当前屏幕的像素指针
- for(int i=0;i
-
-
-
-这里大致说一下每一个文件的作用(虽然后续有重构的可能性):
-
-1. CommonUtils.cpp。用来存放一些通用函数,比如说读取图片之类的。
-2. MathUtils.cpp。用来存放数学相关的函数,比如说计算MVP矩阵,插值等。
-3. Renderer.cpp。渲染相关代码,用来管理渲染的物体以及调用渲染管线渲染等。
-4. Shader.cpp。存放shader代码。
-5. ShadingPipeline.cpp。渲染管线代码,生成渲染结果。
-6. Structure.cpp。定义vetex, frament 以及 mesh的数据类型。
-7. WindowApp.cpp。SDL2相关函数。
-
-> 关于Renderer 和ShadingPipeline 以及 Shader 的组织问题:
->
-> 关于这三个类的所属关系大概是:
->
-> ShadingPipeline 是 Renderer的一个成员,同时 Shader 是 Shadingpipeline的一个成员。
->
-> Renderer主要负责管理场景里的Mesh,同时调用Shadingpipeline去渲染。
->
-> ShadingPipeline主要负责渲染管线的一整套流程,比如说根据vertices indices 构建三角形,比如说光栅化。
->
-> Shader主要负责实现自己的vertexShader以及FragmentShader函数。
-
-## 2. 具体细节
-
-### 2.1 像素展示
-
-基本上可以把渲染的整个过程抽离为 生成像素buffer -> 显示像素buffer。显示像素buffer这个部分就交给了SDL2来做,只需要在每一帧的时候把一个像素数组传递给SDL2就可以展示了,所以我们的渲染器所需要的就是在每一帧生成出这个像素数组就可以了。这里的选取是非常随意的,在GAMES101里使用的opencv来把结果存成图片,[这位大佬的博客](https://yangwc.com/2019/05/01/SoftRenderer-Rasterization/)使用了qt来展示结果,后来他后续把代码重构了,也是使用的SDL2。
-
-比如说其实核心就是 `updateCanvas`这个函数:
-
-```cpp
-void WindowApp::updateCanvas(uint8_t* pixels, int width, int height, int channel) {
- SDL_LockSurface(windowSurface);
- Uint32* surfacePixels = (Uint32*)windowSurface->pixels; //获取当前屏幕的像素指针
- for(int i=0;i -
-
-
- -
-
diff --git a/CG/SoftRasterizer/shading.md b/CG/SoftRasterizer/shading.md
deleted file mode 100644
index 6f67b7f..0000000
--- a/CG/SoftRasterizer/shading.md
+++ /dev/null
@@ -1,517 +0,0 @@
----
-title: 软光栅器MicroRenderer(三) 着色器(完结)
-date: 2022-06-01 12:06:00
-tags: [MicroRenderer]
----
-# 软光栅器MicroRenderer(三) 着色器
-代码见:https://github.com/LJHG/MicroRenderer
-
-本节会对软渲染器剩下的内容进行说明,主要包括:
-1. 模型加载
-2. 贴图uv颜色采样
-3. 更加复杂的shader的设计,本项目中主要实现了 Gouraud shader以及Phong shader。
-
-
-
-## 1. 模型加载
-
-首先来看一下Mesh这个类都包含哪些成员变量:
-
-```cpp
-class Mesh{
-public:
- Mesh();
-
- /** getter and setter for vertices and indices **/
- std::vector
-
-
diff --git a/CG/SoftRasterizer/shading.md b/CG/SoftRasterizer/shading.md
deleted file mode 100644
index 6f67b7f..0000000
--- a/CG/SoftRasterizer/shading.md
+++ /dev/null
@@ -1,517 +0,0 @@
----
-title: 软光栅器MicroRenderer(三) 着色器(完结)
-date: 2022-06-01 12:06:00
-tags: [MicroRenderer]
----
-# 软光栅器MicroRenderer(三) 着色器
-代码见:https://github.com/LJHG/MicroRenderer
-
-本节会对软渲染器剩下的内容进行说明,主要包括:
-1. 模型加载
-2. 贴图uv颜色采样
-3. 更加复杂的shader的设计,本项目中主要实现了 Gouraud shader以及Phong shader。
-
-
-
-## 1. 模型加载
-
-首先来看一下Mesh这个类都包含哪些成员变量:
-
-```cpp
-class Mesh{
-public:
- Mesh();
-
- /** getter and setter for vertices and indices **/
- std::vector -
-意思就是你用windowSurface时就不能再去调其它的3D图形的API了
-
-但是Imgui调用的`SDL_GL_SwapWindow(window)`刚好就是
-
-```cpp
-/**
- * Update a window with OpenGL rendering.
- *
- * This is used with double-buffered OpenGL contexts, which are the default.
- *
- * On macOS, make sure you bind 0 to the draw framebuffer before swapping the
- * window, otherwise nothing will happen. If you aren't using
- * glBindFramebuffer(), this is the default and you won't have to do anything
- * extra.
- *
- * \param window the window to change
- *
- * \since This function is available since SDL 2.0.0.
- */
-extern DECLSPEC void SDLCALL SDL_GL_SwapWindow(SDL_Window * window);
-```
-
-所以这两个函数应该是不能同时调的,我的实验结果就是`SDL_UpdateWindowSurface(window)`会覆盖掉`SDL_GL_SwapWindow(window)`,不论先后。
-
-中途我还尝试了一下用opengl的`glDrawPixels`搞了半天,但是没搞定,我也不知道咋回事,opengl真不熟。
-
-但是解决方案其实也是有的,比如说把要展示的图片弄成一个opengl的2D贴图,然后传给`Imgui::Image()`,但是,又是opengl... 我顶不住了orz。
-
-有人也给出了相关的实现[【Dear imgui】有关Image的实现_Gary的面包屑小道的博客-CSDN博客](https://blog.csdn.net/DY_1024/article/details/105690739),但是最后好像他也没能够把图片弄在背景里,而是搞到一个小窗口里了。
-
-总之先这样吧,反正我个人感觉软渲染器加上Imgui会有点臃肿而且**麻烦**,如果有一天我熟练掌握了opengl,或者vulkan...? 到时候这可能也不是啥问题了。🤔
\ No newline at end of file
diff --git a/CG/imgui_run.md b/CG/imgui_run.md
deleted file mode 100644
index dbcef4d..0000000
--- a/CG/imgui_run.md
+++ /dev/null
@@ -1,52 +0,0 @@
----
-title: 如何将imgui跑起来
-date: 2022-09-05 15:58:31
-tags: [imgui]
----
-
-# 如何将imgui跑起来
-
-不得不说imgui的新手指引真的太劝退了,居然没有一个傻瓜式的直接用cmake编译的例子,这对于cmake小白(我)来说太不友好了。加之imgui本身支持很多后端(opengl, vulkan, metal...),第一眼看过去根本不知所措,我连要include哪些文件都不知道。
-
-于是,在经过一天多的摸索后,我终于把imgui跑起来了。
-
-
-
-意思就是你用windowSurface时就不能再去调其它的3D图形的API了
-
-但是Imgui调用的`SDL_GL_SwapWindow(window)`刚好就是
-
-```cpp
-/**
- * Update a window with OpenGL rendering.
- *
- * This is used with double-buffered OpenGL contexts, which are the default.
- *
- * On macOS, make sure you bind 0 to the draw framebuffer before swapping the
- * window, otherwise nothing will happen. If you aren't using
- * glBindFramebuffer(), this is the default and you won't have to do anything
- * extra.
- *
- * \param window the window to change
- *
- * \since This function is available since SDL 2.0.0.
- */
-extern DECLSPEC void SDLCALL SDL_GL_SwapWindow(SDL_Window * window);
-```
-
-所以这两个函数应该是不能同时调的,我的实验结果就是`SDL_UpdateWindowSurface(window)`会覆盖掉`SDL_GL_SwapWindow(window)`,不论先后。
-
-中途我还尝试了一下用opengl的`glDrawPixels`搞了半天,但是没搞定,我也不知道咋回事,opengl真不熟。
-
-但是解决方案其实也是有的,比如说把要展示的图片弄成一个opengl的2D贴图,然后传给`Imgui::Image()`,但是,又是opengl... 我顶不住了orz。
-
-有人也给出了相关的实现[【Dear imgui】有关Image的实现_Gary的面包屑小道的博客-CSDN博客](https://blog.csdn.net/DY_1024/article/details/105690739),但是最后好像他也没能够把图片弄在背景里,而是搞到一个小窗口里了。
-
-总之先这样吧,反正我个人感觉软渲染器加上Imgui会有点臃肿而且**麻烦**,如果有一天我熟练掌握了opengl,或者vulkan...? 到时候这可能也不是啥问题了。🤔
\ No newline at end of file
diff --git a/CG/imgui_run.md b/CG/imgui_run.md
deleted file mode 100644
index dbcef4d..0000000
--- a/CG/imgui_run.md
+++ /dev/null
@@ -1,52 +0,0 @@
----
-title: 如何将imgui跑起来
-date: 2022-09-05 15:58:31
-tags: [imgui]
----
-
-# 如何将imgui跑起来
-
-不得不说imgui的新手指引真的太劝退了,居然没有一个傻瓜式的直接用cmake编译的例子,这对于cmake小白(我)来说太不友好了。加之imgui本身支持很多后端(opengl, vulkan, metal...),第一眼看过去根本不知所措,我连要include哪些文件都不知道。
-
-于是,在经过一天多的摸索后,我终于把imgui跑起来了。
-
- -
-首先,如果要将imgui导入你的项目,你需要将整个imgui项目导入你的项目中,比如这样:
-
-
-
-首先,如果要将imgui导入你的项目,你需要将整个imgui项目导入你的项目中,比如这样:
-
- -
-然后你需要编写相关的CmakeLists...
-
-```cmake
-cmake_minimum_required(VERSION 3.21)
-project(imgui_demo)
-
-set(CMAKE_CXX_STANDARD 14)
-
-find_package(glfw3 REQUIRED) # 添加glfw
-find_package(GLEW REQUIRED) # 添加glew
-
-include_directories(imgui)
-include_directories(imgui/backends)
-
-add_executable(imgui_demo
- main.cpp
- imgui/imgui.cpp
- imgui/imgui_draw.cpp
- imgui/imgui_tables.cpp
- imgui/imgui_demo.cpp
- imgui/imgui_widgets.cpp
- imgui/backends/imgui_impl_glfw.cpp
- imgui/backends/imgui_impl_opengl3.cpp
- )
-
-target_link_libraries(imgui_demo glfw GLEW::GLEW)
-```
-
-你需要确定自己要用什么后端来跑,这里我们就选择最简单的opengl好了,那么你就需要导入 glfw+glew(这里我是这么选的,其实也可以glfw + glad ?),总之你需要确定自己需要确定自己要导入什么库。
-
-接着include相关的文件夹,再在add_executable里确定相关的文件就可以跑了。。。
-
-这里的main.cpp我选择了imgui官方提供的example_glfw_opengl3里的main.cpp来跑。
-
diff --git a/CPP/README.md b/CPP/README.md
deleted file mode 100644
index 154b140..0000000
--- a/CPP/README.md
+++ /dev/null
@@ -1 +0,0 @@
-整理一些CPP相关的知识
\ No newline at end of file
diff --git a/CPP/compiler_speedUp.md b/CPP/compiler_speedUp.md
deleted file mode 100644
index 2fcf3f1..0000000
--- a/CPP/compiler_speedUp.md
+++ /dev/null
@@ -1,232 +0,0 @@
----
-title: 一些CPP简单的提速方法
-date: 2022-06-18 18:00:00
-tags: [CPP]
----
-# 一些CPP简单的提速方法
-
-最近看了小彭老师的c++课[第四讲](https://www.bilibili.com/video/BV12S4y1K721/?spm_id_from=333.788&vd_source=c0c1ccbf42eada4efb166a6acf39141b), 讲的是c++的编译器优化,打开了新世界的大门。
-
-在这里简单记录一下作业里面我用到的优化方法。
-
-> 在windows wsl2平台进行测试,CPU为i7-6700HQ, 从上至下迭代优化
->
-> > 为什么不在macOS测试捏?macOS SOA居然比AOS慢,完全搞不懂为什么,放弃。
-
-### 不做任何优化:1570ms
-
-首先贴一下官方的源程序:
-
-```cpp
-#include
-
-然后你需要编写相关的CmakeLists...
-
-```cmake
-cmake_minimum_required(VERSION 3.21)
-project(imgui_demo)
-
-set(CMAKE_CXX_STANDARD 14)
-
-find_package(glfw3 REQUIRED) # 添加glfw
-find_package(GLEW REQUIRED) # 添加glew
-
-include_directories(imgui)
-include_directories(imgui/backends)
-
-add_executable(imgui_demo
- main.cpp
- imgui/imgui.cpp
- imgui/imgui_draw.cpp
- imgui/imgui_tables.cpp
- imgui/imgui_demo.cpp
- imgui/imgui_widgets.cpp
- imgui/backends/imgui_impl_glfw.cpp
- imgui/backends/imgui_impl_opengl3.cpp
- )
-
-target_link_libraries(imgui_demo glfw GLEW::GLEW)
-```
-
-你需要确定自己要用什么后端来跑,这里我们就选择最简单的opengl好了,那么你就需要导入 glfw+glew(这里我是这么选的,其实也可以glfw + glad ?),总之你需要确定自己需要确定自己要导入什么库。
-
-接着include相关的文件夹,再在add_executable里确定相关的文件就可以跑了。。。
-
-这里的main.cpp我选择了imgui官方提供的example_glfw_opengl3里的main.cpp来跑。
-
diff --git a/CPP/README.md b/CPP/README.md
deleted file mode 100644
index 154b140..0000000
--- a/CPP/README.md
+++ /dev/null
@@ -1 +0,0 @@
-整理一些CPP相关的知识
\ No newline at end of file
diff --git a/CPP/compiler_speedUp.md b/CPP/compiler_speedUp.md
deleted file mode 100644
index 2fcf3f1..0000000
--- a/CPP/compiler_speedUp.md
+++ /dev/null
@@ -1,232 +0,0 @@
----
-title: 一些CPP简单的提速方法
-date: 2022-06-18 18:00:00
-tags: [CPP]
----
-# 一些CPP简单的提速方法
-
-最近看了小彭老师的c++课[第四讲](https://www.bilibili.com/video/BV12S4y1K721/?spm_id_from=333.788&vd_source=c0c1ccbf42eada4efb166a6acf39141b), 讲的是c++的编译器优化,打开了新世界的大门。
-
-在这里简单记录一下作业里面我用到的优化方法。
-
-> 在windows wsl2平台进行测试,CPU为i7-6700HQ, 从上至下迭代优化
->
-> > 为什么不在macOS测试捏?macOS SOA居然比AOS慢,完全搞不懂为什么,放弃。
-
-### 不做任何优化:1570ms
-
-首先贴一下官方的源程序:
-
-```cpp
-#include  -
-用通俗易懂的话来说就是,给定一个source矩阵,和一个index矩阵,选定一个维度,根据index矩阵从source矩阵里**挑一些值**来作为结果(self)。
-
-于是用下面两行代码就可以生产一个one-hot矩阵:
-
-```python
-one_hot_gt = torch.zeros(batch_size,sequence_size,256)
-one_hot_gt = one_hot_gt.scatter_(dim=2,index=gt.reshape(batch_size,sequence_size,1).data.long().cpu(),value=1)
-```
-
-解释一下:
-
-1. 首先,生成一个全零的`batch_size * sequence_size * classes`形式的矩阵。
-2. 对于`scatter_`函数的参数说明一下。`dim=2`是因为要在最后一维做one-hot。由于输入的index(gt)和self(one_hot_gt)需要维度一致,所以我们将它reshape一下,变为 `batch_size * sequence_size * 1`。`value=1`是因为要把所有的值都替换为1,这也就是source。
-
-如此操作就可以达成以下的效果:
-
-```python
-one_hot_gt[i][j][gt[i][j][0]] = 1 # gt[i][j][0]就是类别的编号
-```
-
-### 后续操作
-
-一旦生成了one-hot矩阵,后续的操作就很简单了,完整的代码如下:
-
-```python
-# 首先将 gt 修改为one-hot形式 (batch_size, sequence_size, 256)
-one_hot_gt = torch.zeros(batch_size,sequence_size,256)
-one_hot_gt = one_hot_gt.scatter_(dim=2,index=gt.reshape(batch_size,sequence_size,1).data.long().cpu(),value=1)
-# 将one_hot_gt和pred点乘
-ans = torch.mul(one_hot_gt.cuda(),pred.cuda())
-# 将所有的0替换为1
-ans[ans == 0] = 1
-ans = -torch.log2(ans).sum()
-```
-
-最后测试得到,原本要3s的运算只需要0.1s了~
\ No newline at end of file
diff --git a/MLDLRL/README.md b/MLDLRL/README.md
deleted file mode 100644
index a22727d..0000000
--- a/MLDLRL/README.md
+++ /dev/null
@@ -1 +0,0 @@
-相关的文章整理得不多,所以把ML/DL/RL这几个部分的文章整理在一起
\ No newline at end of file
diff --git a/MLDLRL/RL/README.md b/MLDLRL/RL/README.md
deleted file mode 100644
index 8cc3fa7..0000000
--- a/MLDLRL/RL/README.md
+++ /dev/null
@@ -1,3 +0,0 @@
-不会强化学习,但是也会学习一些相关的知识。
-
-* [value&policy iteration](value&policy_iteration.md)
\ No newline at end of file
diff --git a/MLDLRL/RL/value&policy_iteration.md b/MLDLRL/RL/value&policy_iteration.md
deleted file mode 100644
index a796448..0000000
--- a/MLDLRL/RL/value&policy_iteration.md
+++ /dev/null
@@ -1,89 +0,0 @@
----
-title: 值迭代和策略迭代
-date: 2021-11-27
-tags: [强化学习]
----
-最近的随机过程作业涉及到了value iteration和policy iteration,于是就去搜了相关的网课[CS229-lecture17](https://www.youtube.com/watch?v=d5gaWTo6kDM)来看,讲的很好,于是做了一些笔记。
-由于这些东西和强化学习能扯上一点关系,所以就分类到了强化学习。
-
-### 关于π和$$V^{\pi}$$
-
-π是optimal polocy,是一个state -> action 的映射
-
-比如:
-
-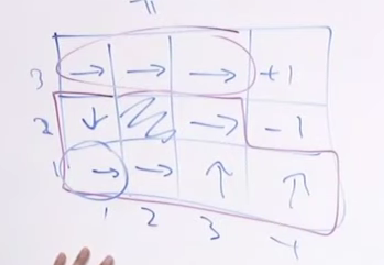
-
-$$V^{\pi}$$ 是 从某一个位置开始(当作初始位置) 所获得的一个 reward
-
-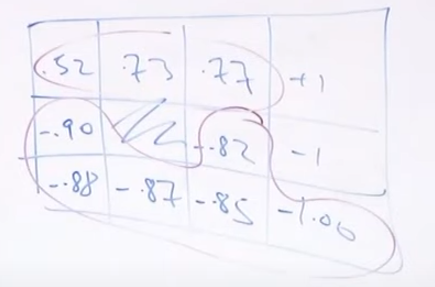
-
-
-
-
-
-#### bellman equation
-
-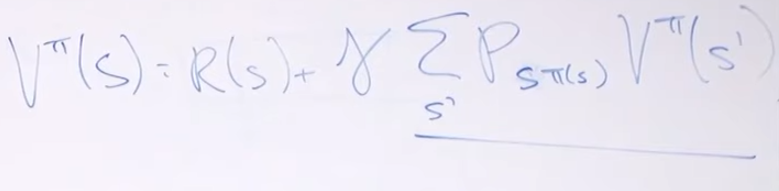
-
-
-
-#### 例子
-
-比如说要求 (3,1) 这个位置的 $$V^{\pi}$$
-
-
-
-那么求法就是:
-
-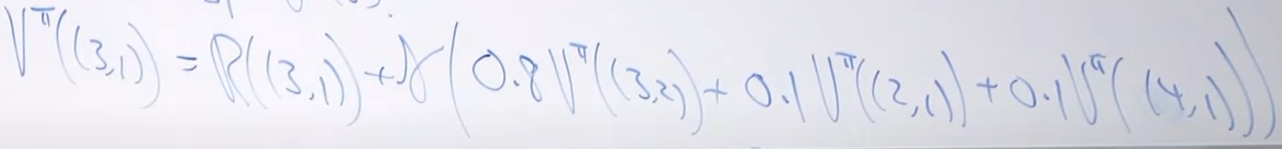
-
-如果把每一个状态对应的$$V^{\pi}$$当作是一个未知数,由于已经给出了确定的policy $$\pi$$ (也就是说action是确定的),那么根据bellman equation,每一个$$V^{\pi}$$都可以写出一个方程。所以可以用一个linear solver来构建方程并且求解。
-
-
-
-
-
-### 关于$$\pi^*$$ 和 $$V^*$$
-
-$$\pi^*$$ 是 optimal policy
-
-$$ V^* $$是 optimal policy 对应的value function,公式如下:
-
-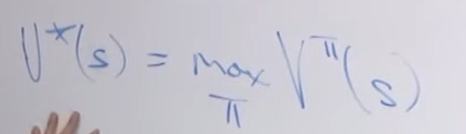
-
-#### 对应的bellman equation
-
-
-
-
-
-### value iteration
-
-由于V(s)直接存在相互依赖关系,value iteration有两种,一种是 synchrounous,就是每一个V(s)同步更新,另一种就是asynchrounous,就是V(s)的更新不同步。不过都差不多。
-
-
-
-经过多次迭代,V就会很快收敛到V*。最后收敛完毕后,再去计算对应的 π(s) 。
-
-
-
-### policy iteration
-
-policy iteration的重点在于π,在循环中。
-
-第一步:根据 π(s) 计算出对应的V。 如何计算? -> 如前面所述,使用linear solver来计算。
-
-第二步:假设V是optimal value function,即V*,然后更新 π(s)。
-
-
-
-
-
-### pros and cons of two methods
-
-由于policy iteration实际是一个 linear solver based 的 方法,所以当状态数很少时,求解速度很快,但是当状态数目很多时,求解速度就会变慢。所以在状态数目很多时,倾向于使用 value iteration。
-
-
-
-
diff --git a/README.md b/README.md
deleted file mode 100644
index 83e0bad..0000000
--- a/README.md
+++ /dev/null
@@ -1,7 +0,0 @@
-# jh的个人站
-
-我的知识整理站点,什么都写一点。
-
-> 从PaperMod白嫖过来的logo :D
-
-
-
-用通俗易懂的话来说就是,给定一个source矩阵,和一个index矩阵,选定一个维度,根据index矩阵从source矩阵里**挑一些值**来作为结果(self)。
-
-于是用下面两行代码就可以生产一个one-hot矩阵:
-
-```python
-one_hot_gt = torch.zeros(batch_size,sequence_size,256)
-one_hot_gt = one_hot_gt.scatter_(dim=2,index=gt.reshape(batch_size,sequence_size,1).data.long().cpu(),value=1)
-```
-
-解释一下:
-
-1. 首先,生成一个全零的`batch_size * sequence_size * classes`形式的矩阵。
-2. 对于`scatter_`函数的参数说明一下。`dim=2`是因为要在最后一维做one-hot。由于输入的index(gt)和self(one_hot_gt)需要维度一致,所以我们将它reshape一下,变为 `batch_size * sequence_size * 1`。`value=1`是因为要把所有的值都替换为1,这也就是source。
-
-如此操作就可以达成以下的效果:
-
-```python
-one_hot_gt[i][j][gt[i][j][0]] = 1 # gt[i][j][0]就是类别的编号
-```
-
-### 后续操作
-
-一旦生成了one-hot矩阵,后续的操作就很简单了,完整的代码如下:
-
-```python
-# 首先将 gt 修改为one-hot形式 (batch_size, sequence_size, 256)
-one_hot_gt = torch.zeros(batch_size,sequence_size,256)
-one_hot_gt = one_hot_gt.scatter_(dim=2,index=gt.reshape(batch_size,sequence_size,1).data.long().cpu(),value=1)
-# 将one_hot_gt和pred点乘
-ans = torch.mul(one_hot_gt.cuda(),pred.cuda())
-# 将所有的0替换为1
-ans[ans == 0] = 1
-ans = -torch.log2(ans).sum()
-```
-
-最后测试得到,原本要3s的运算只需要0.1s了~
\ No newline at end of file
diff --git a/MLDLRL/README.md b/MLDLRL/README.md
deleted file mode 100644
index a22727d..0000000
--- a/MLDLRL/README.md
+++ /dev/null
@@ -1 +0,0 @@
-相关的文章整理得不多,所以把ML/DL/RL这几个部分的文章整理在一起
\ No newline at end of file
diff --git a/MLDLRL/RL/README.md b/MLDLRL/RL/README.md
deleted file mode 100644
index 8cc3fa7..0000000
--- a/MLDLRL/RL/README.md
+++ /dev/null
@@ -1,3 +0,0 @@
-不会强化学习,但是也会学习一些相关的知识。
-
-* [value&policy iteration](value&policy_iteration.md)
\ No newline at end of file
diff --git a/MLDLRL/RL/value&policy_iteration.md b/MLDLRL/RL/value&policy_iteration.md
deleted file mode 100644
index a796448..0000000
--- a/MLDLRL/RL/value&policy_iteration.md
+++ /dev/null
@@ -1,89 +0,0 @@
----
-title: 值迭代和策略迭代
-date: 2021-11-27
-tags: [强化学习]
----
-最近的随机过程作业涉及到了value iteration和policy iteration,于是就去搜了相关的网课[CS229-lecture17](https://www.youtube.com/watch?v=d5gaWTo6kDM)来看,讲的很好,于是做了一些笔记。
-由于这些东西和强化学习能扯上一点关系,所以就分类到了强化学习。
-
-### 关于π和$$V^{\pi}$$
-
-π是optimal polocy,是一个state -> action 的映射
-
-比如:
-
-
-
-$$V^{\pi}$$ 是 从某一个位置开始(当作初始位置) 所获得的一个 reward
-
-
-
-
-
-
-
-#### bellman equation
-
-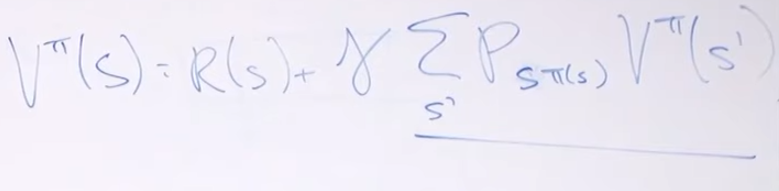
-
-
-
-#### 例子
-
-比如说要求 (3,1) 这个位置的 $$V^{\pi}$$
-
-
-
-那么求法就是:
-
-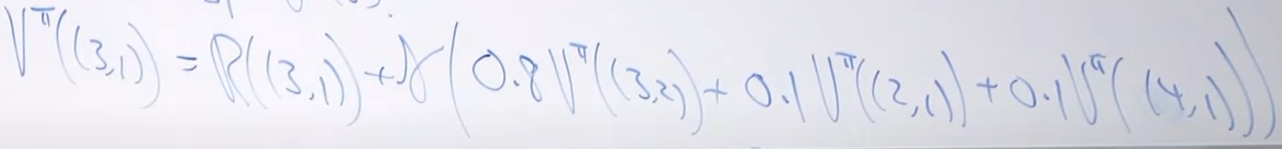
-
-如果把每一个状态对应的$$V^{\pi}$$当作是一个未知数,由于已经给出了确定的policy $$\pi$$ (也就是说action是确定的),那么根据bellman equation,每一个$$V^{\pi}$$都可以写出一个方程。所以可以用一个linear solver来构建方程并且求解。
-
-
-
-
-
-### 关于$$\pi^*$$ 和 $$V^*$$
-
-$$\pi^*$$ 是 optimal policy
-
-$$ V^* $$是 optimal policy 对应的value function,公式如下:
-
-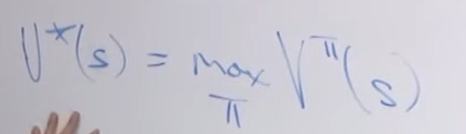
-
-#### 对应的bellman equation
-
-
-
-
-
-### value iteration
-
-由于V(s)直接存在相互依赖关系,value iteration有两种,一种是 synchrounous,就是每一个V(s)同步更新,另一种就是asynchrounous,就是V(s)的更新不同步。不过都差不多。
-
-
-
-经过多次迭代,V就会很快收敛到V*。最后收敛完毕后,再去计算对应的 π(s) 。
-
-
-
-### policy iteration
-
-policy iteration的重点在于π,在循环中。
-
-第一步:根据 π(s) 计算出对应的V。 如何计算? -> 如前面所述,使用linear solver来计算。
-
-第二步:假设V是optimal value function,即V*,然后更新 π(s)。
-
-
-
-
-
-### pros and cons of two methods
-
-由于policy iteration实际是一个 linear solver based 的 方法,所以当状态数很少时,求解速度很快,但是当状态数目很多时,求解速度就会变慢。所以在状态数目很多时,倾向于使用 value iteration。
-
-
-
-
diff --git a/README.md b/README.md
deleted file mode 100644
index 83e0bad..0000000
--- a/README.md
+++ /dev/null
@@ -1,7 +0,0 @@
-# jh的个人站
-
-我的知识整理站点,什么都写一点。
-
-> 从PaperMod白嫖过来的logo :D
-
- -
-## 实现细节
-
-详细代码请见:[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-实现了main.cpp中的**get_model_matrix**, **get_rotation**, **get_projection_matrix**函数。
-
-其中每一个的实现基本都能在下面的相关知识找到对应,无非就是把矩阵用代码写出来了而已。
-
-这里记录一个需要注意的点,就是在**get_projection_matrix**函数中,在设置**n**和**f**(近平面和远平面)时,需要加一个负号:
-
-```cpp
-float n = -zNear;
-float f = -zFar;
-```
-
-
-
-
-# 相关知识
-
-
-
-## 关于三维的变换
-
-### 一般的旋转变换
-
-[旋转变换(一)旋转矩阵_Frank的专栏-CSDN博客_旋转变换矩阵](https://blog.csdn.net/csxiaoshui/article/details/65446125)
-
-### 绕任意轴的旋转变换
-
-
-
-## 实现细节
-
-详细代码请见:[详细代码](https://github.com/LJHG/GAMES101-assignments)
-
-实现了main.cpp中的**get_model_matrix**, **get_rotation**, **get_projection_matrix**函数。
-
-其中每一个的实现基本都能在下面的相关知识找到对应,无非就是把矩阵用代码写出来了而已。
-
-这里记录一个需要注意的点,就是在**get_projection_matrix**函数中,在设置**n**和**f**(近平面和远平面)时,需要加一个负号:
-
-```cpp
-float n = -zNear;
-float f = -zFar;
-```
-
-
-
-
-# 相关知识
-
-
-
-## 关于三维的变换
-
-### 一般的旋转变换
-
-[旋转变换(一)旋转矩阵_Frank的专栏-CSDN博客_旋转变换矩阵](https://blog.csdn.net/csxiaoshui/article/details/65446125)
-
-### 绕任意轴的旋转变换
-
- -
-## MVP
-
-### M: Model transformation
-
-模型变化,**应该**就是指模型的变化。包括平移、旋转、放缩等等操作。
-
-在本次的作业中指的就是绕z轴旋转,这对应一个变换矩阵。
-
-
-
-### V: View transformation
-
-视图变换,指的就是从相机出发观测物体,那么就需要将相机移动到原点,并且面朝-z方向,向上方向为y轴正方向。
-
-将相机移动后,我们需要也对物体做一个移动,来保持相对位置不变。所以最后的结果就是,我们直接假定相机在原点,面朝-z方向,向上方向为y轴正方向,然后**只对物体做这个变换**就行了。
-
-
-
-## MVP
-
-### M: Model transformation
-
-模型变化,**应该**就是指模型的变化。包括平移、旋转、放缩等等操作。
-
-在本次的作业中指的就是绕z轴旋转,这对应一个变换矩阵。
-
-
-
-### V: View transformation
-
-视图变换,指的就是从相机出发观测物体,那么就需要将相机移动到原点,并且面朝-z方向,向上方向为y轴正方向。
-
-将相机移动后,我们需要也对物体做一个移动,来保持相对位置不变。所以最后的结果就是,我们直接假定相机在原点,面朝-z方向,向上方向为y轴正方向,然后**只对物体做这个变换**就行了。
-
-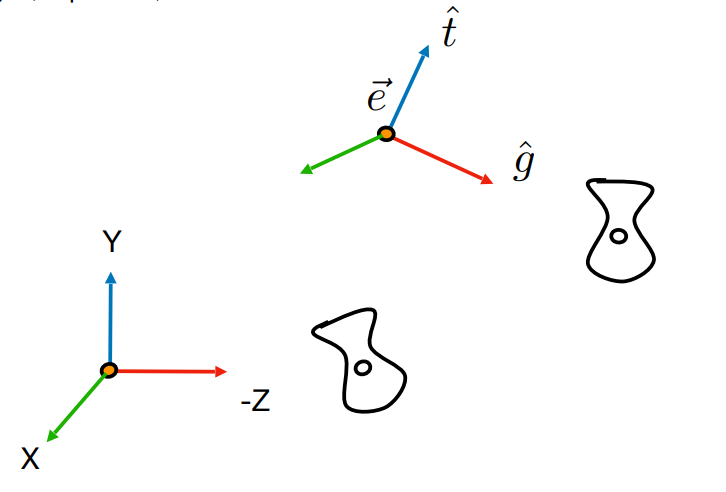 -
-该变换分为两步:
-
-这里我们把视图变换的矩阵令为 $$M_{view}$$ ,平移矩阵令为 $$T_{view}$$ ,旋转矩阵令为 $$R_{view}$$
-
-1. 将相机移动到原点
-
- 平移矩阵为 $$T_{view}$$
-
-
-
-该变换分为两步:
-
-这里我们把视图变换的矩阵令为 $$M_{view}$$ ,平移矩阵令为 $$T_{view}$$ ,旋转矩阵令为 $$R_{view}$$
-
-1. 将相机移动到原点
-
- 平移矩阵为 $$T_{view}$$
-
-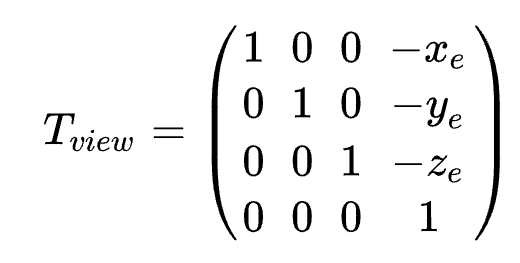 -
-2. 将相机旋转到面朝-z方向,且上方为y正方向。
-
- 直接对$$R_{view}$$ 进行求解比较困难,所以我们转而去求它的逆变换,即将处于原点,面向-z,上朝y的相机旋转到当前的相机位置,用$$R_{view}^{-1}$$表示,那么有:
-
-
-
-2. 将相机旋转到面朝-z方向,且上方为y正方向。
-
- 直接对$$R_{view}$$ 进行求解比较困难,所以我们转而去求它的逆变换,即将处于原点,面向-z,上朝y的相机旋转到当前的相机位置,用$$R_{view}^{-1}$$表示,那么有:
-
-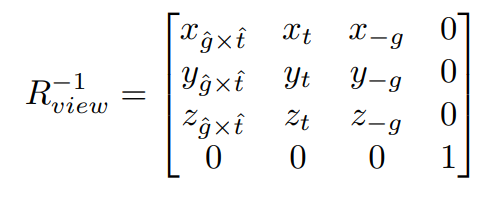 -
- 因为旋转矩阵是一个正交矩阵,所以矩阵的逆等于矩阵的转置,因此我们可以求得$$R_{view}$$:
-
-
-
- 因为旋转矩阵是一个正交矩阵,所以矩阵的逆等于矩阵的转置,因此我们可以求得$$R_{view}$$:
-
-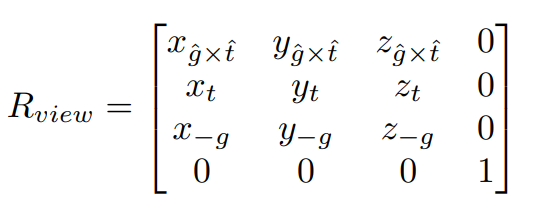 -
-因为模型变换和视图变化都是在物体上进行变化,所以一般我们把他们一起叫做**模型视图变换**。
-
-
-
-### P:Perspective projection
-
-#### 正交投影(Orthographic projection)
-
-正交投影就是在空间中确定一个立方体 (用来表示相机的可视区域),对应六个面在不同坐标轴下的距离为right, left, top, bottom, near, far,要做的事情就是把这个立方体移动到原点,并且缩放到 (-1, 1)。
-
-
-
-因为模型变换和视图变化都是在物体上进行变化,所以一般我们把他们一起叫做**模型视图变换**。
-
-
-
-### P:Perspective projection
-
-#### 正交投影(Orthographic projection)
-
-正交投影就是在空间中确定一个立方体 (用来表示相机的可视区域),对应六个面在不同坐标轴下的距离为right, left, top, bottom, near, far,要做的事情就是把这个立方体移动到原点,并且缩放到 (-1, 1)。
-
-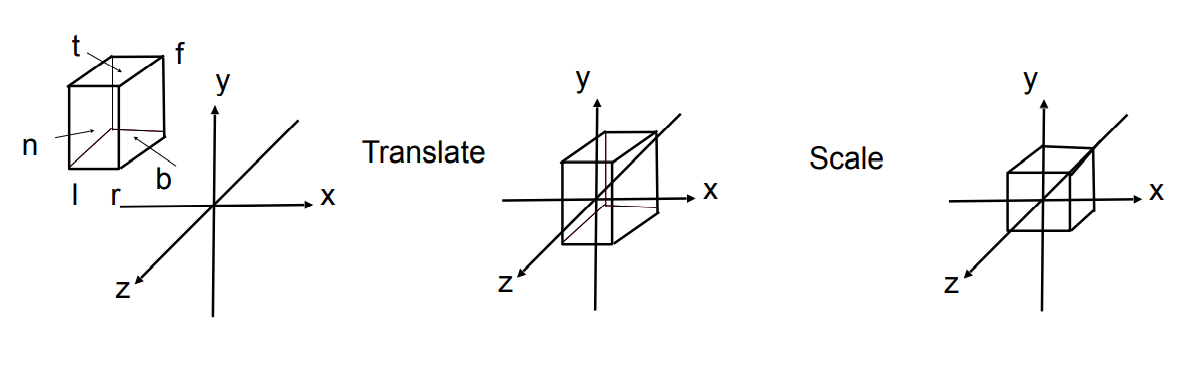 -
-对应的矩阵$$M_{ortho}$$ 为:
-
-
-
-对应的矩阵$$M_{ortho}$$ 为:
-
-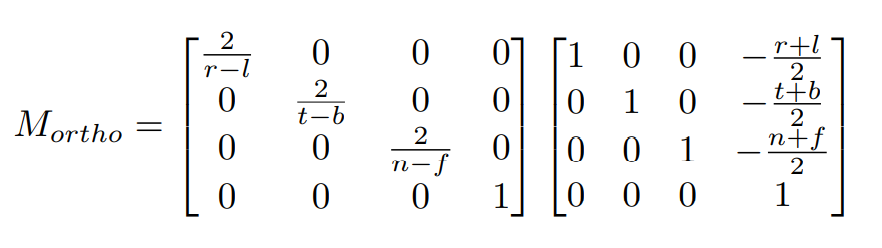 -
-#### 透视投影(Perspective projection)
-
-##### 矩阵推导
-
-透视投影就是将正交投影里面的一个立方体变成了一个forstum,我们要做的就是先将这个forstum "挤" 成一个立方体,然后后续操作就和正交投影一样了。
-
-
-
-#### 透视投影(Perspective projection)
-
-##### 矩阵推导
-
-透视投影就是将正交投影里面的一个立方体变成了一个forstum,我们要做的就是先将这个forstum "挤" 成一个立方体,然后后续操作就和正交投影一样了。
-
- -
-其中,透视投影变换矩阵为 $$M_{persp}$$ ,我们只需要去求透视投影向正交投影的变换矩阵 $$M_{persp->ortho}$$ 即可
-
-
-
-其中,透视投影变换矩阵为 $$M_{persp}$$ ,我们只需要去求透视投影向正交投影的变换矩阵 $$M_{persp->ortho}$$ 即可
-
-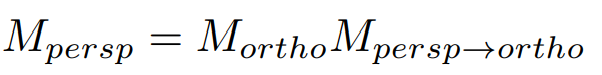 -
-$$M_{persp->ortho}$$ 的求法比较发杂,下面贴一些图:
-
-* 对于当$$M_{persp->ortho}$$ 作用到(x,y,z,1)后,对于frostum里的每一个点,可以得到:
-
-
-
-$$M_{persp->ortho}$$ 的求法比较发杂,下面贴一些图:
-
-* 对于当$$M_{persp->ortho}$$ 作用到(x,y,z,1)后,对于frostum里的每一个点,可以得到:
-
-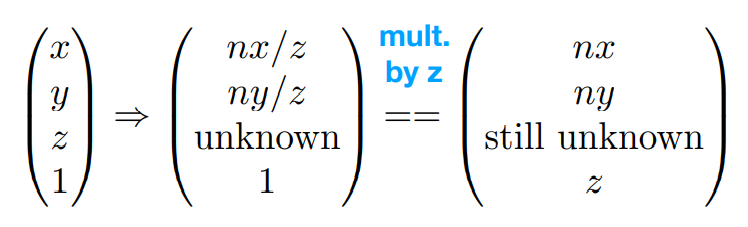 -
-* 根据这个,我们已经可以得出矩阵中的大部分元素
-
-
-
-* 根据这个,我们已经可以得出矩阵中的大部分元素
-
- -
-* 再根据下面标红的两个发现(近平面的点不会变,远平面的z不会变)列出公式,求解最后剩余的?
-
-
-
-* 再根据下面标红的两个发现(近平面的点不会变,远平面的z不会变)列出公式,求解最后剩余的?
-
- -
-
-
- -
-
-
- -
-
-
- -
-于是就求解得到$$M_{persp->ortho}$$ 了。
-
-
-
-##### fov与aspect ratio
-
-fov是(field of view),即竖直方向的可视角度
-
-aspect ratio是width/height
-
-只需要使用fov和aspect ratio就可以用来表示一个透视投影(n和f是给定的,所以我们再把fov和aspect ratio转换为l, r, b, t即可)
-
-
-
-
-
-于是就求解得到$$M_{persp->ortho}$$ 了。
-
-
-
-##### fov与aspect ratio
-
-fov是(field of view),即竖直方向的可视角度
-
-aspect ratio是width/height
-
-只需要使用fov和aspect ratio就可以用来表示一个透视投影(n和f是给定的,所以我们再把fov和aspect ratio转换为l, r, b, t即可)
-
-
-
-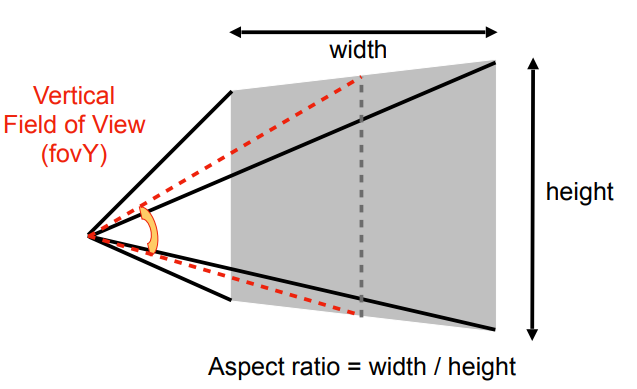 -
-
-
-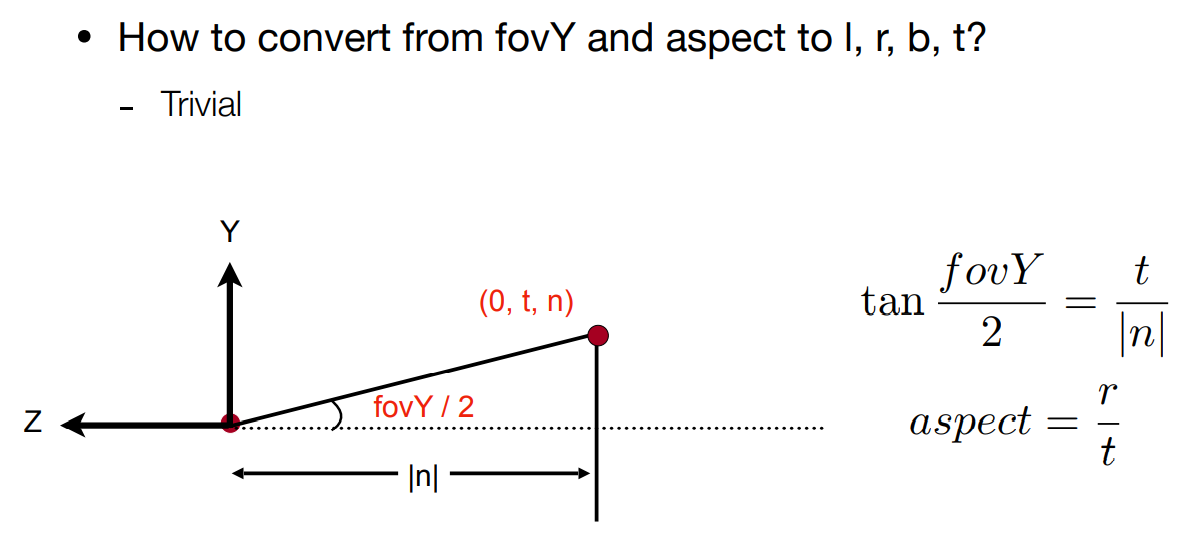 -
diff --git a/CG/GAMES101/assignment2.md b/CG/GAMES101/assignment2.md
deleted file mode 100644
index 02bbd7f..0000000
--- a/CG/GAMES101/assignment2.md
+++ /dev/null
@@ -1,86 +0,0 @@
----
-title: GAMES101-assignment2-ZBuffuer
-date: 2021-11-11
-tags: [GAMES101]
----
-# Assignment2
-
-## 运行结果
-
-
-
diff --git a/CG/GAMES101/assignment2.md b/CG/GAMES101/assignment2.md
deleted file mode 100644
index 02bbd7f..0000000
--- a/CG/GAMES101/assignment2.md
+++ /dev/null
@@ -1,86 +0,0 @@
----
-title: GAMES101-assignment2-ZBuffuer
-date: 2021-11-11
-tags: [GAMES101]
----
-# Assignment2
-
-## 运行结果
-
- -
-
-
-
-
-## 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-我认为这次的assignment的重点有三个:
-
-1. 三角形内的判断
-2. 三角形边界的确定
-3. 深度buffer
-
-
-
-### 1. 三角形内的判断
-
-判断一个点是否在三角形内是通过叉乘来判断的,假设一个点为**P**,我们与三角形的三个顶点相连,并分别令为**PA**,**PB**,**PC**,那么需要计算**PAPB**, **PBPC**, **PCPA**的叉乘,只要三个结果同号,那么该点就在三角形内。这里需要注意一下叉乘的顺序,倘若把**PCPA**写为**PAPC**,结果就会大不相同。
-
-```cpp
-static bool insideTriangle(int x, int y, const Vector3f* _v)
-{
- //TODO : Implement this function to check if the point (x, y) is inside the triangle
-
- //suppose the coordinate of p is (x,y)
-
- x = x + 0.5f;
- y = y + 0.5f;
- std::pair
-
-
-
-
-
-## 实现细节
-
-[详细代码](https://github.com/LJHG/GAMES101-assignments)
-我认为这次的assignment的重点有三个:
-
-1. 三角形内的判断
-2. 三角形边界的确定
-3. 深度buffer
-
-
-
-### 1. 三角形内的判断
-
-判断一个点是否在三角形内是通过叉乘来判断的,假设一个点为**P**,我们与三角形的三个顶点相连,并分别令为**PA**,**PB**,**PC**,那么需要计算**PAPB**, **PBPC**, **PCPA**的叉乘,只要三个结果同号,那么该点就在三角形内。这里需要注意一下叉乘的顺序,倘若把**PCPA**写为**PAPC**,结果就会大不相同。
-
-```cpp
-static bool insideTriangle(int x, int y, const Vector3f* _v)
-{
- //TODO : Implement this function to check if the point (x, y) is inside the triangle
-
- //suppose the coordinate of p is (x,y)
-
- x = x + 0.5f;
- y = y + 0.5f;
- std::pair -
-
-
-## 解题思路
-
-这道题是贪心,用两个位置来表示区间,并且判断左右两边的大小,并且移动小的那一边。
-
-这个方法很好想,好像可以通过反证法去证明它不是错的。。。
-
-至于dp,这道题差点我又dp了,但是一看数据范围开不了二维dp,那也dp不了了。
-
-```cpp
-class Solution {
-public:
- int maxArea(vector
-
-
-
-## 解题思路
-
-这道题是贪心,用两个位置来表示区间,并且判断左右两边的大小,并且移动小的那一边。
-
-这个方法很好想,好像可以通过反证法去证明它不是错的。。。
-
-至于dp,这道题差点我又dp了,但是一看数据范围开不了二维dp,那也dp不了了。
-
-```cpp
-class Solution {
-public:
- int maxArea(vector